COVID-19 感染者数の傾向

更新履歴
2022 Dec.31
日本国内向けデータ元を厚生労働省へ変更したことを追記。

1. 概要

本アプリは、公開されているCOVID-19感染者数データを元に、グラフ作成向けにデータ整理するものである。
簡単なグラフ描画機能もアプリに付属しているが、感染者数データを国別、あるいは都道府県別に時系列データとしてcsvファイルに出力する。なお、本ページ内に示した図は、本アプリにて出力したcsvデータをExcelでグラフ化したものである。

感染者数等のデータ元は表1-1に示す4つである。なお、日本国内向けデータとして、2022年12月31日現在、更新されているものは厚生労働省のみである。したがって、最新版のアプリも、日本国内向けデータとしては厚生労働省のみを扱うようになっている。

補足として、感染者数データ公開の経緯を書いておく。
まず、最も早く自国の統一的なデータを公開したのは Johns Hopkins University である。アメリカの大学なので、まずはアメリカをはじめとして主要国のデータを公開した。この中には日本も含まれていたが、初期の段階では全国感染者数のみであった。

日本国内の統一的な感染者数データを最初に公開したのは、ジャッグジャパン株式会社 (J.A.G JAPAN Corp.) である。Johns Hopkins University の表現方法を参考にして、画面上の見栄えは同形式で公開した。一方、個々の感染者数データは人数のみならず、性別や年代など各保健所の報告する詳細なデータも含まれていた。しかし、国内感染者の増加率が多くなってくると、データ収集に労力がかかるのか更新頻度が落ちていき、2020年11月30日を最後に更新が止まっている。一方、この時期には厚生労働省が一応のデータを公開したことと (しかし、csv等の形式で統一的に扱える公開の方法ではない) 、NHKも統一的なデータを公開し始めており、ジャッグジャパン株式会社は自分の役目を終えたと判断したのだろう。

ジャッグジャパン株式会社が更新を停止して以降、ユーザがデータ整理を行えるような感染者数データを公開していたのは、NHKだけである。そんなNHKも、2022年9月27日に更新を停止した。理由は、厚生労働省がようやくまともなデータを公開し始めたからである。

この経緯を振り返ると、日本の公的機関の情けなさを感じずにはいられない。国内感染者数が飛躍的に増加するなかで、公的機関の情報は各市町村や県どまりで、全国データを把握するまでにかなりの手間を要した。そのような中で、真っ先に統一的なデータを公開したのは民間のジャッグジャパン株式会社だけであった。本来厚生労働省などの公的機関がやるべき仕事だと思うが、結局彼らがまともなデータを公開したのは、それから2年半以上経過した2022年9月27日以降である。その間しびれを切らしたのか、NHKが中継ぎしていた、ということである。

表1-1：本アプリで用いたCOVID-19感染者数のデータ元

No.	データ元	対象	備考
1	Johns Hopkins University	全世界向けデータ	図1-1
2	NHK	日本国内向けデータ	図1-2, 現在は更新停止
3	ジャッグジャパン株式会社 (J.A.G JAPAN Corp.)	日本国内向けデータ	図1-3, 現在は更新停止
4	厚生労働省	日本国内向けデータ	図1-4

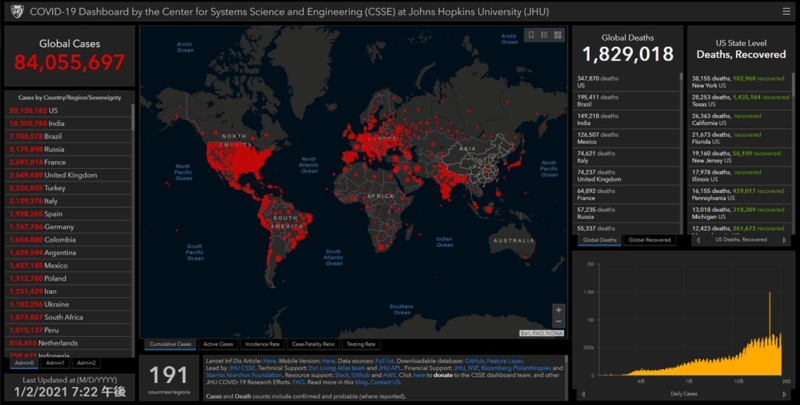
図1-1：データ元(1) Johns Hopkins University <全世界向けデータ>

図1-2：データ元(2) NHK <日本国内向けデータ>

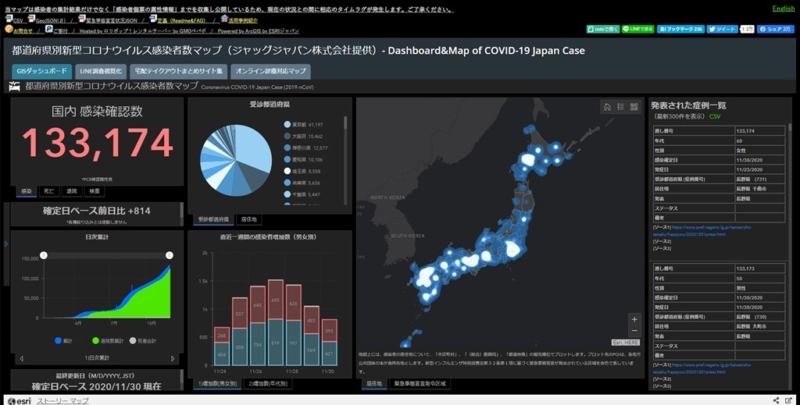
図1-3：データ元(3) ジャッグジャパン株式会社 (J.A.G JAPAN Corp.) <日本国内向けデータ>

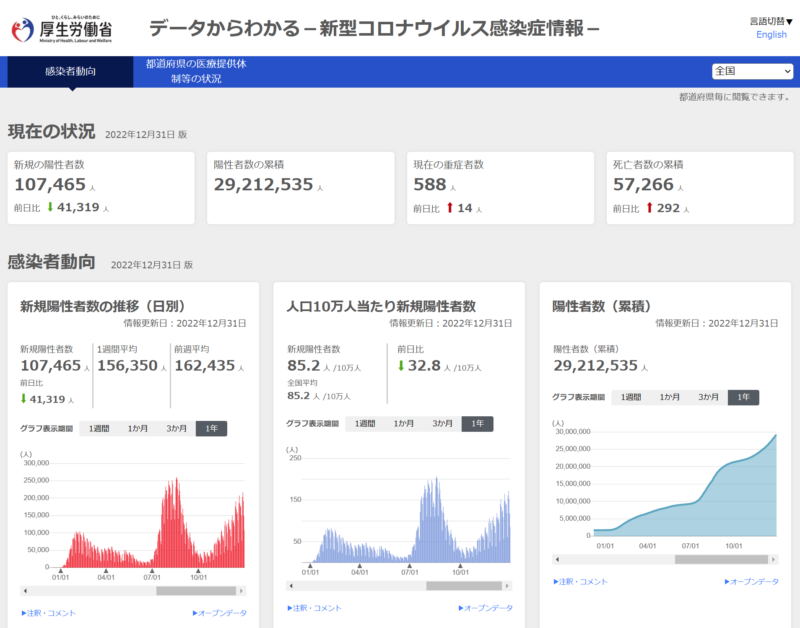
図1-4：データ元(4) 厚生労働省 <日本国内向けデータ>

2. Download

Windows PC版、Android版の2つがある。
Windows PC版は Windows 11 にて、Android版は Android 13 にて、それぞれ動作確認を実施している。

なお、Android版の簡易グラフ描画機能は1系列のみである。

Android版はGoogle Playでの公開を予定していたが、現在COVID-19関連のアプリはGoogle Playでの公開を許可されていない(正式な政府機関によって公開、委託、または直接承認されている必要がある)。これに気づいたのはアプリ作成後だったのだが、どうしようもないので、自サイトで公開することとした。

図2-1：アプリアイコン

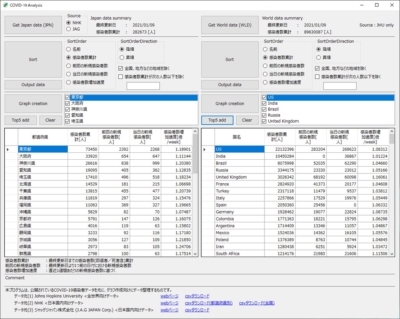
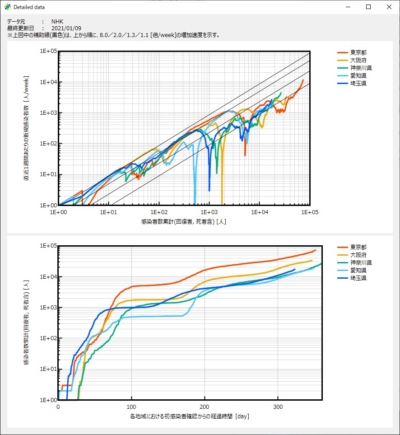
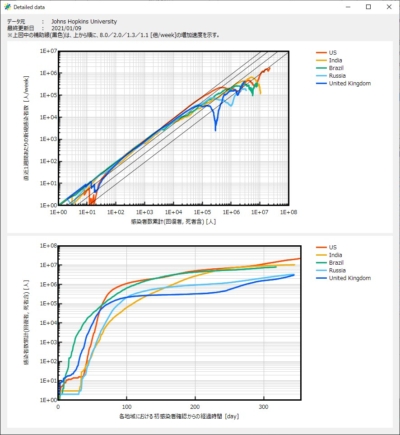
図2-2：PC版スクリーンショット

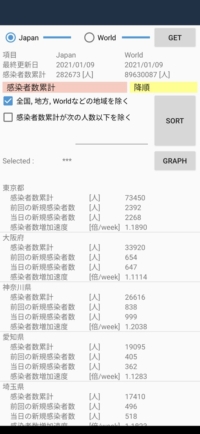
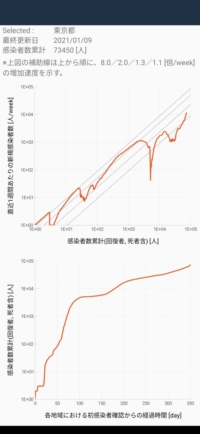
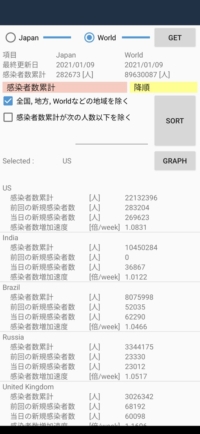
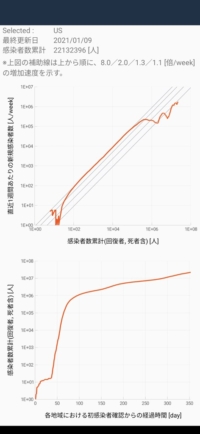
図2-3：Android版スクリーンショット

3. 詳細

まず、図3-1を見てほしい。
横軸は感染者数累計、縦軸は直近1週間あたりの新規感染者数として、東京都のデータ(2021 Jan.10 現在)をプロットしている。軸はいずれも常用対数(底が10)をとってある。なぜ対数をとるかは後で述べるが、規則的な増加速度、例えば1週間あたり感染者数累計が2倍／3倍／4倍…となるようなラインは、このグラフでは傾き1の直線となり増加速度の差異は上下のシフト量で表される。図中の黒実線で示す4種類の補助線がそれである。

このようにして見ると、東京都の増加速度は、最大値が約8倍/weekを超えていたこと、また増加速度の大きな低減が3回あったこと、そして今時点(2021 Jan.10 現在)において増加速度の低減は見られず、その増加速度は約1.1倍/weekを超えていることが分かる。ウイルスを完全に抑制できたとき、新規感染者数=0 となるので、この図では下に落ち込むことを意味する。

図3-1：東京都の感染者数の傾向
(データ元：NHK, 2021 Jan.10 時点のデータ)

さて、同じデータを普通のグラフ(横軸／縦軸ともリニア)で示したものが図3-2である。
おそらく、報道等で最もよく見かけるグラフだろう。図3-2における生値の振動周期はおおよそ1週間なのだが、これは人間の活動サイクルが同じく1週間だからであろう。そのため、直近1週間の平均データも示しており、傾向を評価していく上ではこちらの平均値データを用いる方が望ましいと考える。

図3-2から読み取れるのは、大きな山が2つあり、3つ目の山が作られようとしている、ということだけで、増加速度の変化を読み取るのは困難である。つまり、1日当たりの新規感染者数が前日と比較して増加した／減少した、という情報は、増加速度を全体的に把握するうえであまり意味のない情報なのだ。これは前述の生値の振動の問題もあるが、たとえ平均値で評価しても、前日より新規感染者数が多いから増加速度は大きくなった、とは必ずしも言えないのである。
後に数学的な裏付けを記載するが、定性的には感染者数累計は指数関数的に増加すると考えられるので、1日当たりの新規感染者数も指数関数的に増加することになる。すなわち、増加速度が一定であっても、日々の新規感染者数は一定とならず指数関数的に増加していくが、これは当たり前のことなのである。指数関数は日常生活で接する機会は少ないが、通常のリニアスケールとは感覚的に全く異なるものである。我々の関心は、増加速度が上昇するのか／減少するのか、であり、これを評価するには図3-1で示したようなグラフを用いると容易にできる。

図3-2：東京都の新規感染者数推移
(データ元：NHK, 2021 Jan.10 時点のデータ)

さて、図3-1に示したグラフで、各国の感染者数の傾向を比較してみよう。感染者数累計のワースト5(2021 Jan.10 時点)を図3-3に示す。驚くべきことに、感染者数累計が約1万人に達するまでは各国とも同程度の増加速度(約8.0倍/week)であることが分かる。また、United Kingdom は、感染者数累計が10万人を超えたあたりでこの増加速度から脱出しているが、その後再び増加速度が戻ってきている。その他の国も程度の差はあれど同様の傾向である。

図3-3：各国の感染者数の傾向(感染者数累計ワースト5)
(データ元：JHU, 2021 Jan.10 時点のデータ)

もう一つ例を示す。今度は増加速度ベスト5(感染者数累計10万人以上の国)を図3-4に示す。
当然だが、各国とも増加ラインから脱出し、それを維持しているのが分かる。

図3-4：各国の感染者数の傾向(増加速度ベスト5, 感染者数累計10万人以上の国)
(データ元：JHU, 2021 Jan.10 時点のデータ)

図3-3／図3-4に示すように、このようなプロットを用いると、感染者数累計の異なる各国の状況を容易に評価することができる。図3-4では下方向への落ち込みが分かりやすいように”感染者数累計10万人以上の国”と条件を付けたが、もっと少ない国でも同じグラフで評価できる。これは、このグラフの取り方が、(1)対数プロットを用いていることと、(2)時間に対してプロットしていないこと、が大きな効果を生んでいる。

(1)については、対数というものは小さい数を拡大し、大きい数を縮小する、という性質を持ち、大きな幅に広がっているデータの比較を容易にしてくれる。工学的にも、指数関数的物理現象について対数プロットはよく用いられている。

(2)については、このグラフに時間項が陽的に出ていないことに注目してほしい。我々は時間に対して感染者数等を関連付けてしまうが、ウイルスにとって時間は重要ではないのだ。もちろん、ウイルスが体内に侵入して発病、その人間が感染力を持つまでにはいくらか時間を要するので、その観点では時間は意味のあるものだ。だが、他者への感染は主に人間の交流活動の活発さに依存しているといえるだろう。どんなに感染力の強いウイルスであっても、人間が交流活動を一切しなければ新規感染者数は増えないのだから。

グラフから時間を消すことで、ウイルス本来の感染性能および各国の抑制への取り組みの効果を、より見出しやすいものとなっている。例えば図3-3で、「感染者数累計が約1万人に達するまでは各国とも同程度の増加速度(約8.0倍/week)である」と述べたが、これはつまり、人間の交流活動を特に制限しない場合のウイルスの感染力は約8倍/weekの増加速度を持つ、と言えるだろう。また、各国の比較で、同じ感染者数累計であっても増加ラインからいち早く脱出しているか、あるいは同じ増加速度のまま増えてしまっているか、の差異は、つまるところ、その国のCOVID-19に対する政策であったり、国民性が反映されていると言ってもよいだろう。(ただし、厳密には時間経過に伴いウイルス性能が変化(変異)する可能性はある。)
未だ増加ラインから脱出できない国にとって、増加ラインから脱出した国のとった政策などは、何か参考になるのではないだろうか。

上記のようにグラフの説明を行ったが、このグラフは私が考えたものではなく、海外Youtuberの方が紹介されていた内容である。以下にそのリンクを示すので、興味のある方はぜひ見てほしい。私が本アプリを作ったのも、このグラフが革命的に素晴らしいものだと感動し、それを自分でもデータ整理してみたかったからである。(1)の対数プロットの着想は工学系ならまず思いつく内容だが、(2)の時間を消す着想は全く思いつかなかった。ウイルスの性質と数式を深く理解した素晴らしいものだと思う。

図3-5：How To Tell If We’re Beating COVID-19 (by minutephysics)

4. 数学的補足

ウイルスの感染は、感染者が非感染者にある距離ある時間接触した場合、ある確率 \(p\) で起きるものとする。
すなわち、

$$ p=f(接触距離, 接触時間, etc, \cdots) \tag{4-1} $$

と表現できるだろう。これがウイルス固有の性能である。
一方、人間の交流活動の活発さを \(h\) とすれば、

$$ h=f(単位時間当たりの他人との平均接触距離, \\
平均接触時間, etc, \cdots) \tag{4-2} $$

と表現できるだろう。ここで、増加速度(単位時間あたり感染者数累計が何倍になるか)を \(k\) とすると、人間が交流しなければ感染しないのだから、

$$ k=f(p,h) \tag{4-3} $$

と表せる。1日当たりあるいは1週間当たり、感染者数累計が〇〇倍になる、この〇〇という値が \(k\) に相当するものである。一般に、伝染病というものは単位時間あたりに感染者数が〇〇倍、という具合に増加していく。例えば、感染者は1日あたり必ず1人の非感染者を感染させると考えると( \(k\) =2に相当)、感染者数累計は1日経過ごとに、最初の日の感染者数の、2倍、4倍、8倍、16倍、…、と増えていくからである。(図4-1)

図4-1：k=2の場合の感染者数増加のイメージ

ウイルスが突然変異しない場合、\(p\) は一定なので \(k\) は \(h\) のみの関数となる。

$$ k=f(h) \quad ※ウイルスが突然変異しない場合 \tag{4-4} $$

すなわち、\(k\) を読み取ることができれば、その地域のとったウイルス対策が有効に機能しているか(人間の交流活動を抑制できているか)、を定量的に評価できるのである。(ただしウイルスは突然変異しない前提)

経過時間、感染者数累計および増加速度を、以下のように定義する。

\begin{alignat}{2}
x \quad & \colon \; 初感染者確認からの経過時間 & \qquad \qquad \qquad & [week] \\
y \quad & \colon \; 感染者数累計 & & [人] \tag{4-5} \\
k \quad & \colon \; 感染者数累計の増加速度 & & [倍/week]
\end{alignat}

単位時間は \(day\) でもよいのだが、図3-2に示したように、1 \(day\) あたりの新規感染者数は振動することが多いため、単位時間は \(week\) として評価する。
感染者数累計 \(y\) は感染力を持つ人間の数であり(厳密には死者は入らず、また回復者も入らないかもしれないが、今は簡単に考えていずれも含むとする)、単位時間あたり感染者数累計が \(k\) 倍していくのだから、\(x\) と \(y\) には次の関係がある。

$$ y=k^x \tag{4-6} $$

我々が知りたいのは、増加速度 \(k\) であり、これをグラフから容易に読み取れるようにしたい。
まず、指数関数がどういうグラフになるか見てみよう。底の異なる指数関数を図4-2に示すが、\(x\) の増加に伴い \(y\) は急激に増加していく。これが指数関数の特徴である。

例えば、1分間に1回細胞分裂を行い2個に増殖する細菌を考える。容器内にこの細菌を1個入れて1時間経過したとき、容器内がこの細菌で満杯になった。では、容器の半分がこの細菌で満たされたときはいつだろうか。感覚的には30分経過時かもしれないが、ちょっと待ってほしい。この細菌は1分間で自分の個数を2倍にできる能力を持つ。だから、容器の半分がこの細菌で満たされたときは59分経過時、すなわち、たった1分前なのである。

このように指数関数は驚異的な速度で増加していく。そして、この増加曲線を通常のグラフに描画して(図4-2)人間の目で評価することは困難であることも分かる。(図4-2から増加係数(指数関数の底)が2.0なのか2.2なのか、ということは容易に読み取れないだろうし、そもそも \(y=x^2\) のような冪関数と誤解する可能性すらある。)

図4-2：指数関数の様子

一方、図4-2と同じ指数関数を片対数でプロットしたものを図4-3に示す。(片対数というのは、グラフ軸2つのうちの片方という意味で、通常は \(Y\) 軸を対数とする)

なんと、指数関数が直線になっているではないか。これなら傾きから容易に係数を読み取れるだろう。
しかしこれは、どいう仕組みなのだろうか。

図4-3：指数関数の様子(Y軸 対数)

\(y\) の対数をとってみる。

\begin{align}
\begin{split}
y&=k^x \\
\log_{10} y &=x\log_{10} k=ax \\
\end{split}
\tag{4-7}
\end{align}

ここで、
$$ a=\log_{10} k \tag{4-8} $$
と置く。
また、\(X\) 軸, \(Y\) 軸を

\begin{align}
\begin{split}
X \quad & \colon \; X軸 \\
Y \quad & \colon \; Y軸
\end{split}
\tag{4-9}
\end{align}

と表すことにする。今、\(Y\) 軸は対数をとるので、

\begin{align}
\begin{split}
X &= x \\
Y &= \log_{10} y = ax = aX
\end{split}
\tag{4-10}
\end{align}

と表せる。すなわち、\(Y\) は \(X\) の一次関数となる。
したがって、\(Y\) 軸を対数とした片対数プロットにて表すと、傾き \(a\) の直線となる。

いろいろ書いたが、感染者数累計 \(y\) は、定性的には経過時間 \(x\) の指数関数として表され、またそれを片対数プロットするとその増加速度 \(k\) に応じて直線の傾きが異なることが分かった。早速、実データを用いてプロットしてみる。東京都の感染者数累計を示したものが図4-4であり、(a)は通常のグラフ、(b)は片対数プロットである。この2つのグラフは、全く同じデータをプロットしていることに注意してほしい。

2つのグラフを比較するとどうだろうか。図4-4(a)では、感染者数がどんどん増加していくことくらいしか読み取れなさそうだが、図4-4(b)では増加速度がその曲線の傾き(=接線)をイメージすることで読み取ることができる。具体的には、約100日経過付近で増加速度はいったん収束に向かい、その後上昇するがその速度は100日以前より小さい、etc…ということが分かるだろう。

図4-4：東京都の感染者数累計
(データ元：NHK, 2021 Jan.10 時点のデータ)

さらに、複数の系列をプロットしてみる。感染者数累計ワースト3の都道府県の片対数プロットを図4-5に示す。
さきほどと同様に、増加速度を読み取ることはできるのだが、相対比較がうまくできなくなってきたようだ。

ここで、ウイルス感染の本質を思い出そう。3章で述べたとおり、ウイルスにとって時間は重要ではない。

我々は時間に対して感染者数等を関連付けてしまうが、ウイルスにとって時間は重要ではないのだ。もちろん、ウイルスが体内に侵入して発病、その人間が感染力を持つまでにはいくらか時間を要するので、その観点では時間は意味のあるものだ。だが、他者への感染は主に人間の交流活動の活発さに依存しているといえるだろう。どんなに感染力の強いウイルスであっても、人間が交流活動を一切しなければ新規感染者数は増えないのだから。

3章より

これはしかし、如何にして時間項を消し、人間の目に分かりやすいようなグラフを作ることができるのだろうか。

図4-5：国内感染者数累計ワースト3都道府県(Y軸 対数)
(データ元：NHK, 2021 Jan.10 時点のデータ)

直近単位時間あたりの新規感染者数 \(\Delta y\) を考えてみよう。これは現在から単位時間前の感染者数累計との差異であるから、

\begin{align}
\begin{split}
x \quad & \colon \; 初感染者確認からの経過時間 & \qquad \qquad \qquad & [week] \\
y \quad & \colon \; 感染者数累計 & & [人] \\
k \quad & \colon \; 感染者数累計の増加速度 & & [倍/week] \\
\Delta y \quad & \colon \; 直近単位時間当たりの新規感染者数 & \qquad \qquad \qquad & [人/week]
\end{split}
\tag{4-11}
\end{align}

$$ y=k^x \tag{4-6} $$

\begin{align}
\begin{split}
\Delta y &= k^x – k^{x-1} \\
&= k^x \left( 1 – \frac{1}{k} \right) \\
&= y \left( 1 – \frac{1}{k} \right)
\end{split}
\tag{4-12}
\end{align}

となる。つまり、直近単位時間あたりの新規感染者数 \(\Delta y \) は、感染者数累計 \(y\) の一次関数となる。
大きな範囲に存在するデータを扱うため、やはり対数を用いたい。\(\Delta y \) の対数をとると、

$$ \log_{10} \Delta y = \log_{10} y + \log_{10} \left( 1 – \frac{1}{k} \right) \tag{4-13} $$

となる。
ここで、X軸, Y軸を次のように選べば、

\begin{align}
\begin{split}
X &= \log_{10} y \\
Y &= \log_{10} \Delta y = X + \log_{10} \left( 1 – \frac{1}{k} \right)
\end{split}
\tag{4-14}
\end{align}

と表せる。時間項 \(x\) を陽的に表していないことが分かる。
また、増加速度 \(k\) に依らず傾きは1となる。\(k\) の違いは、上下のシフト量(切片)として表されるのである。実はこの効果が絶大である。百聞は一見に如かず、さきほどと全く同じデータ(図4-5)を、この方法でプロットしたものを図4-6に示す。

さてどうだろう。相対比較を行うと、感染者数累計が100人以下の領域では、神奈川県、東京都、大阪府の順に増加ラインから脱出している。すなわち、同じ感染者母数で評価すれば、大阪府はこの区間の中で最悪であることが分かる。
感染者数累計が千人付近、1万人付近の領域では、増加速度は東京がワーストである。
また、最後のデータ点、すなわち2021 Jan.10 付近の傾向を見るに、いずれも増加速度に低下の傾向が見られないことも分かる。

2021年は、これはまた大変な年になりそうである…。

図4-6：国内感染者数累計ワースト3都道府県(両対数)
(データ元：NHK, 2021 Jan.10 時点のデータ)