お天気お姉さんからの質問にガチ解答する

1. 概要

自分が良く見ている天気予報番組「ウェザーニュースLiVE」にて、お天気お姉さんから視聴者へ、熱力学の質問が出された。彼女が気象予報士の資格取得の勉強をしていたところ、熱力学の問題に突き当たったのだという。なるほど、たしかに気象現象にも熱は絡んでいる。番組内の解説員 (気象予報士) との会話にて一応の解決はみたものの、熱屋からみると腑に落ちない部分がある。

本記事では、お天気お姉さんの質問に対し、曖昧な表現を用いず、熱力学の範疇からガチ解答を行う。もちろん、ガチ解答などお天気お姉さんは望んでいないだろうから、最初はシンプルな解答（高校物理レベル）を示し、その後、詳細を含めたガチ解答を示す。

2. 関連文書

ガチ解答をするにあたり、言葉の定義などを自分の言葉で正確に表現することが困難なので、いくつかの文献から引用しながら説明していく。本記事の関連文書を下表に示す。

No.	文書番号など
1	押田勇雄, 藤城敏幸 (1988).『熱力学（改訂版）』. 裳華房.
2	絶対温度とは何か (積分因子とは何か). (n.d.). Retrived Aug. 21, 2022 from http://fnorio.com/0101absolute_temperature1/absolute_temperature1.html

3. ウェザーニュースLiVEとは

ウェザーニュースLiVEは、最新の気象・防災情報を迅速かつ的確にお伝えする気象情報専門会社による生動画番組です。

お天気アプリ「ウェザーニュース」をはじめ、YouTube・ニコニコ生放送・LINE LIVE・Abema TVでご覧いただけます。

ウェザーニュースLiVE webページより抜粋

もっとも、自分にとっては、綺麗なお姉さんを見るための番組であり、正直、天気予報は聞いていない。

絶望に満ちた世界を生きるためには、何らかの救いが必要である。俺の場合、それが映画やアニメであることが多かったのだが、数年前からウェザーニュースLiVEも選択肢に入ってきた。

中でも「檜山沙耶」キャスターは、自分の大好きなキャスターの一人であり、今日も生きる元気をもらっている。

新規動画から数年前のものまで、様々な切り抜き動画を視聴していたそんなある日のこと、熱力学の問題が出されたことを知るのだった。

4. お天気お姉さんからの熱力学に関する質問

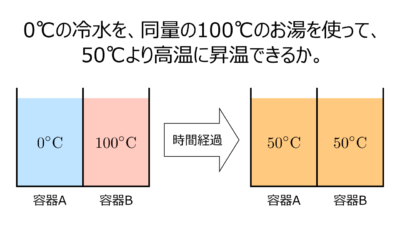
ウェザーニュースLiVEキャスターの檜山氏から、下図の質問が提示された。自分ならどう答えるか、ぜひ考えてみてほしい。いくつか問題点はあるものの、熱力学の根本を問う非常によい問題だと思う。

図4-1：2022.06.03 ウェザーニュースLiVE 檜山沙耶 [815]ム＠SAYArchive 38ch
（2:32:50～）

図4-1の放送にて、\(\Delta W\) を「デルタワット」と言っているが、これは誤りで、\(W\) はアルファベット読みで、「ダブリュー」と言う。「ワット」と言ってしまうと、単位時間当たりの発熱量を意味する別のものになってしまう。なお、後述するように、\(Q, W\) に対して \(\Delta\) を付けるべきではない。
また、\(C_p\) の添え字 \(p\) のことを単位 \(\mathrm{[Pa]}\) 由来と言ってるが、これも誤りで、正しくは圧力を意味する pressure 由来である。

5. 解答

内容としては高校物理の熱力学の内容なのだが、正確に答えるためには熱力学の重要な考え方である「状態量」を理解しなければならない。

また、実は問題自体に誤りがあり、これに気付く必要がある。

まず、5.1節に問題文の誤りに言及し、5.2節にシンプルな解答を、5.3節にガチ解答をそれぞれ示す。

5.1 問題文の誤り

この問題文には致命的な誤りがある。後日の放送にて、以下のように訂正された。

図5.1-1：2022.06.07 ウェザーニュースLiVE 檜山沙耶 [818]ム＠SAYArchive 38ch
（1:44:56～）

すなわち、

\begin{align}
& 誤：\, & \Delta U &= C_p \Delta T \tag{5.1-1} \\[0.5em]
& 正：\, & \Delta U &= C_V \Delta T \tag{5.1-2}
\end{align}

と訂正された。番組内では、「一部誤解を招くような表現、紛らわしい表現があったということで、一部訂正させていただきます」と言っているが、これは明らかに誤記である。

しかし、たとえこの訂正が無かったとしても、訂正前の問題 (図4-1) を聞かれた際に、誤りを見抜いた上で、改めて檜山氏の疑問は何かを考え、それに答えるべきである。誤りがあることは大きな問題ではなく、それを読み解いた上で、何を問われているか考えることも、解答者にとっては極めて重要な技術である。誤りを指摘するだけでは単なる批判であり、それでは檜山氏の求める答えにはならないし、淡々と学問上の正解を述べるだけでは、これまた突き放した感があって、避けるべき解答方法である。

本来なら誤記のあった図4-1の問題は省略して、正しい問題である図5.1-1のみを本記事で取り上げるべきかもしれないが、上記のとおり、その誤りに気づくことも重要であると判断し、掲載することにした。

この問題は高校の熱力学で習う初歩レベルの問題であり、また、上記以外にも問題文には不適切な表現がいくつかあるので、分かっている人からすると答える気を失くす問題かもしれない。しかし俺は、自分の生涯に渡って関わり続けている分野である熱力学を取り上げられたことが嬉しく、今まで熱力学に関わってきて良かったと初めて思えた瞬間でもあったので、この問題に対して真面目に向き合うこととした。

5.2 シンプルな解答

本節では問題文の表現を優先して解答しているため、学問上不適切な表現を一部含んでいることに注意を要する。
例えば \(\Delta Q, \Delta W\) とは表現せず、単に \(Q,W\) と表現すべきである。詳細は5.3節のガチ解答を参照のこと。

理想気体 1 mol を前提として、図5.2-1に示すように、ある平衡状態1から平衡状態2へ変化する過程を考える。

図5.2-1：平衡状態の変化の様子

ここで、内部エネルギーは状態量であり、その変化量は経路に依存しない。また、理想気体の内部エネルギーは温度のみに依存するから、\(p_1, p_2,V_1, V_2\) が如何なる値であっても \(T_1, T_2\) が分かっていれば、内部エネルギーの変化は算出できる。そこで、\(T_1\) から \(T_2\) へ変化する過程のうち、最も考えやすい定積変化に着目する。

定積変化では体積が変化しないため仕事はゼロ \(( \Delta W=0)\) であり、問題文に示された熱力学第一法則より、

$$ \Delta Q = \Delta U \tag{5.2-1} $$

となる。すなわち、系に加えられた熱量は全て内部エネルギーの変化に使われる。また、定積変化において、外部から入った熱量は、その定義から、1 mol あたり

$$ \Delta Q = C_V \Delta T \tag{5.2-2} $$

である。

式\(\text{(5.2-1)}\) および 式\(\text{(5.2-2)}\) より、

$$ \Delta U = C_V \Delta T \tag{5.2-3} $$

である。(証明終わり)

ここで注意すべき点は、理想気体を前提として、ある平衡状態1から平衡状態2への変化は、これが定積変化だろうが定圧変化だろうが、あるいは準静的過程でなくとも、内部エネルギーの変化量は 1 mol あたり \(\Delta U = C_V \Delta T\) と表せるということである。
上記の説明では定積変化を用いているが、それは内部エネルギーが状態量であり、平衡状態1と平衡状態2を結ぶ如何なる経路で計算しようともその変化量は同じであり、かつ内部エネルギーは温度のみに依存するから、計算が楽な (仕事がゼロとなる) 定積変化を用いたにすぎず、その結果は定積変化に限定されるものではない。

さらに分かりやすい解答として、教育系YouTuberの予備校のノリで学ぶ「大学の数学・物理」さんの動画を以下に紹介する。注意点として、仕事 \(W\) の向きが逆になっていることと、\(n\) mol 当たりを考えていることが上記と異なる。(ただし、次節に示すように、今回の問題文の表現は学問上一部不適切であり、一般的には下記動画の表記が用いられる)

図5.2-1：高校の熱分野を全部解説する授業【物理】＠予備校のノリで学ぶ「大学の数学・物理」
(1:31:57～)

5.3 ガチ解答

本節では、おそらく誰も望んでいないであろう、学問上のガチ解答を行う。5.1節の解答は とりあえずの解答であり、それで納得できれば何の問題もない。しかし、

• 熱力学第一法則とは何か？
• 状態量とは何か？
• 内部エネルギーとは何か？
• 内部エネルギーが温度のみに依存する根拠は何か？

といった疑問が浮かんでくるかもしれない。これらは、熱力学を作り上げた先人たちも同様に悩み苦しんだものであり、疑問を持つことは自然である。熱力学はその性質上、抽象的なために理解し難いが、裏を返せば、とてつもない普遍性を持っている。

5.3.1 問題文の再整理

前述のように、今回の問題文は学問上不適切な表現を一部含んでいるが、それを以下にまとめる。

1. 状態量ではない \(Q,W\) に\(\Delta\) をつけるべきではない。
2. 1 mol あたり (または 1 kg あたり) と書くべき。
3. 仕事 \(W\) の向きはどちらでもよいが、一般には、外部からなされる仕事を正にとる。
4. 理想気体を前提とすることを明記すべき。

1. について、状態量が何であるかは後に説明するが、記号 \(\Delta\) は「変化」を意味しており、状態量でのみ意味をもつ。状態量でない物理量については、経路によって変化が一意に定まらないから、変化は定義できず、単なる量である。

2. について、一般には、物質量や質量など、注目する気体の量も変数であるから、例えば \(\Delta U = nC_V \Delta T\) と表現する。問題文では \(n\) を省略しているので、1 mol あたり (または1 kg あたり) ということは読み取れるのだが、誤解が無いように明記すべきである。

3. について、一般には外部からなされる仕事を正とする場合が多い。

4. について、実在気体の内部エネルギーは温度のみに依存しないため、容易に表すことはできない。もっとも、定積変化に限定されるのであれば簡略に表現できるが、それでも \(C_V\) は温度依存性があり定数ではないから、問題文のように表現できない。したがって、理想気体を前提とすることを明記すべきである。

以上の議論をまとめ、問題文を再整理すると、以下のような表現となる。

理想気体において、ある平衡状態から温度が \(\Delta T \, \mathrm{[K]}\) 変化して別の平衡状態となったとき、内部エネルギーの変化量は \(\Delta U = n C_V \Delta T\) と表せることを示せ。なお、理想気体の物質量を \(n \, \mathrm{[mol]}\) 、定積モル比熱を \(C_V \, \mathrm{[J/(mol \cdot K)]}\) とする。

5.3.2 熱力学第一法則

熱力学第一法則発見の歴史を、関連文書（1）より抜粋する。

熱力学は、物理学の中の1分野であることはだれでも知っているであろう。一体、熱力学は何を研究する学問なのかは、抽象的な表現をするより、その発展を歴史的に振り返ってみると最もよくわかる。

現在のように熱力学とよべるようになったのは19世紀に入ってからであり、それ以前は単に熱学であった。（中略）人間がこの分野における知識をはじめて充実させ、体系化し、この知識に対してふさわしい物理的解釈を与えたのは、やっと17世紀になってからのことである。それは熱現象を単に観察するだけでなく、実験的に研究しようとするようになったからである。

（中略）特に18世紀に混乱をまねいた熱理論の2つの基本概念である温度と熱を、正確に区別することが可能になった。（中略）しかしながら、その本質が何であるかについては、18世紀の終り頃までは熱を運動の一形態と考える学者と、熱を一種の物質とする熱素説（カロリック説）をとる学者とがあった。（中略）熱素説の正しいか否かの問題を解決することは、一目瞭然たる確実な実験のみがなし得るのであるが、そのような実験は18世紀末になって行われはじめた。特に、

　熱学的現象に力学的現象が加わるような現象を説明するとき、熱素説の欠点が現れたのである。

ことに、熱素説に大きい打撃を与えたのはランフォードの実験であった。すなわち、彼がミュンヘンの造兵廠で大砲作りの監督をしていたとき、砲身を穿孔する際に熱が無尽蔵に出てくることから考えて、 1798年に熱は物質ではなく、運動の中にあると結論を下したのである。

（中略）これらの実験は、これから先いろいろな形で他の学者によってくり返され、いつも熱素説に反することを証明した。上述の実験は、熱というものに関する基本的な概念を根本的に再検討することの発端になった。しかし、習慣的になっていた熱素の概念を学者たちが完全に捨てさることを決意するまでには、さらに幾年かが経過した。たとえば、フランスのカルノーは熱機関の効率を、依然熱素説の立場から説明し、ある程度成功している。

熱が運動の特殊な形態であるという最終的な勝利は、熱の仕事当量の発見によって決定した。

力学の分野で得られたエネルギーの保存則を、熱現象まで含めて明確に把握してはじめて一般的に表明したのは、ドイツの医学者マイヤーであった。彼は人体生理学の問題をきっかけに、この法則に到達したのであった。そして熱の仕事当量がこの法則にとって基本的な定数であることを指摘した。しかし、彼の理論は根拠薄弱であったように思われ、当時の学会には認められなかった。

続いて、イギリスのジュールはマイヤーとは独立に、1843年に仕事当量の測定を試みた。さらにその後もたびたび測定方法を変えて正確な仕事当量の値を得た。こうして熱がエネルギーの一形態であることが量的にも規定されると、クラウジウス、トムソンによって、エネルギー保存則の原理が打ち立てられたのである。一方、 ドイツのヘルムホルツは独立に、ニュートンの運動法則からエネルギー保存則を発表した（1847年）。

　このように熱がエネルギーの一種であるとすると、各種のエネルギーとの関係がどのようになっているかということが問題になる。このような立場から熱現象を取扱う分野を熱力学とよぶようになったのである。

たとえば、熱と力学的エネルギーの間のエネルギー保存則を熱力学第1法則とよんでいる。

熱学ないし熱力学は、エネルギー保存則の確立とともに一層発展した。同時にまた歴史的には17世紀における紡績機の発明と、その動力としての蒸気機関の研究と平行して発展していった。

関連文書（1）より抜粋

熱力学第1法則をとってみても、苦難の歴史がある。熱素説というのは、「熱素」という、目に見えず重さの無い熱の流体があって、これが流れ込むことによって、物体の温度が上昇したりするのだ、という考え方である。当時は、多くの物理学者がこれを信じており、カルノーサイクルの名前の由来となったカルノーでさえも、熱素説の立場から熱機関の効率を論じた。

しかし、前述のとおり、「熱学的現象に力学的現象が加わるような現象を説明するとき、熱素説の欠点が現れ」るのである。すなわち、熱と力学的仕事の間には、何らかの関係が存在することが、経験的事実から明らかとなった。

熱と力学的仕事の関係として、現在用いられる表現は、次式である。

$$ W=JQ \tag{5.3.2-1} $$

ここで、

\begin{alignat}{3}
&Q & \quad & \colon \; 熱量 && \mathrm{[cal]} \\
&W & \quad & \colon \; Q と同等な仕事 & \qquad \qquad \qquad & \mathrm{[J]} \\
&J & \quad & \colon \; 熱の仕事当量 && \mathrm{[J/cal]} \\
\end{alignat}

である。[cal] という単位は、かつては広く用いられたが、現在では、できるだけ使用せず、もし使用する場合には [J] の値を併記することになっている。1 cal は、水 1 g を 1 ℃ 昇温させるのに必要な熱量に相当するが、水の比熱は定数ではなく、温度等に依存するため、測り方によって値が変わってしまう。熱の仕事当量 \(J\) の具体的な値は例えば \(J=4.18605 \) [J/cal] であるが、もちろんこれ以外の値でも間違いではない。おおよそ 4.2 である。

ランフォードやデービーによる前述の実験と、マイヤー、 ジュールによる熱の仕事当量の発見は、熱と仕事とは同等な量で、失なわれた仕事は熱として現れるというものである。もっと正確にいうと、力学的仕事がバーナーの炎や電熱器を物体に当てて、温度を上昇させる（または氷を溶かす） のと等しい効果を与えることができるという重要な法則に到達した。そこで、 エネルギーの概念を拡張して熱を含めると、 この法則は次のようになる。

　熱はエネルギー移動の一形態に対して用いられる用語であり、エネルギー保存の法則は力学的仕事によるエネルギーの移動と、熱の形によるエネルギー移動の総和を考えてはじめて成立する。これを熱力学第1法則という。

はじめ力学において得られたエネルギー保存の法則は、上に述べたように熱現象まで含められることを知ったが、力学的仕事の形のエネルギー移動と熱の形のエネルギー移動とだけを考えたのでは保存則が成り立たない場合がある。しかし、その場合は適当な他の種類（たとえば電気的、磁気的、化学的など）のエネルギーを導入することによって、保存則がいつでも成り立つようにすることができる。

ヘルムホルツは1847年、マイヤー、ジュールとは独立に一般的な立場から、力学的エネルギーの保存則を拡張して、あらゆる種類のエネルギーについても保存されることを示した。そしてある体系のもっているエネルギーの総量は外部とのエネルギーのやりとりがない限り一定で、外部とやりとりのある場合は、その増加は外部から入ったエネルギーの量に等しいというエネルギー保存則を立てた。彼の理論は思想的、数学的にも完全な形でエネルギー保存則に到達した。

関連文書（1）より抜粋

結局のところ、熱力学第1法則はエネルギー保存則である。しかし、従来の力学的エネルギー保存則が熱を含めて拡張可能であることを見出した功績はあまりに大きい。また、要すれば電磁気等の他の種類のエネルギーに対しても拡張可能であり（熱の仕事当量を求めたように、他の種類のエネルギーに対しても仕事当量を求めればよい）、完全な形でのエネルギー保存測に到達する。これは、熱力学の圧倒的な普遍性の一つと言えるだろう。

5.3.3 内部エネルギー

熱力学の最初の方で出てくる「内部エネルギー」の説明を、関連文書（1）より抜粋する。

第1法則によると熱はエネルギーの一形態であるから、高温物体Aの温度が低くなり、低温物体Bの温度が高くなるということは、それに相当するAのエネルギーが減ってBのエネルギーが増加することである。

いまAのもつエネルギーとBのもつエネルギーの総和が変らないとすると、この両物体は、物体全体が運動しているためにもつ運動エネルギーや、高い場所にあるためにもつ位置エネルギーのほかに、温度や圧力などのようなその内部状態によって決まるエネルギーをもっていると考えなければならない。たとえば、体積一定のもとにある1つの物体が外部から熱の形をもったエネルギーをもらえばその物体の温度が上昇する。つまり、この物体のエネルギーは増加する。このように物体の内部の状態によって決まるエネルギーを内部エネルギーという。

（中略）エネルギー保存の法則によると、決まった状態にある物体はある一定の値のエネルギーをもっており、これは上述の内部エネルギーをもっていることになる。したがって、ある系に何かある外部の作用があると、系の内部エネルギーの変化が起こる。

熱力学では内部エネルギーを変化させるのに2つの方法がある。すなわち、仕事を行う場合と電熱器やバーナーの火で熱するような場合である。たとえば、ジュールの実験においては容器の中の水の温度を上昇させるのに、つまり水の内部エネルギーを増加させるのに、おもりを落下させることによって仕事を与えた。しかし、水の加熱は別の方法、たとえばバーナーの火で直接熱することによっても実現できる。

このように、熱力学に内部エネルギーの概念を導入することによって力学的エネルギー保存の法則を非力学的現象にも拡張することができたのである。内部エネルギーを変化させる2つの方法である仕事と熱量とは、内部エネルギーの量を測る尺度であるということができる。

関連文書（1）より抜粋

「内部エネルギー」という新しい概念が出てくるが、熱力学第1法則を認めることによって、必然的にその存在を認めなければならないものである。

分子や原子の存在が明らかになった現代においては、内部エネルギーは物体を構成する分子（または原子）の運動エネルギーと分子間（または原子間）の結合力に関係したこれらの位置エネルギーによって決定されるもので、物体自身の位置（高さなど）や、物体の全体としての状態にはよらない、と言える。

熱力学が確立した19世紀中頃は、原子や分子の存在が広く認められておらず、内部エネルギーが本質的に何かを知ることはできなかった。しかし、これを知らなくても、内部エネルギーの存在を認めることができて、熱力学の理論体系を構築できる点は驚くべきことである。これも、熱力学の圧倒的な普遍性の一つである。

5.3.4 熱力学第1法則の数式化

熱力学第1法則とは、力学的エネルギー保存則を熱にまで拡張したものであった。これは、物体の持つ内部エネルギーの総量は外部のやり取りがない限り不変であり、外部とのやり取りがある場合には、その増加は外部から入った熱量 \(Q\) と、この物体に対して外部からなされる力学的仕事 \(W\) との和に等しいということを意味している。

ある状態1の内部エネルギーを \(U_1\)、状態2の内部エネルギーを \(U_2\) とすると、1から2に移る間にその物体が外から受けるエネルギーは、

$$ U_2 – U_1 = JQ+W \tag{5.3.4-1} $$

と表せる。ここで、\(J\) は熱の仕事当量である。式\(\text{(5.3.4-1)}\) で仕事を \(W \, \mathrm{[J]}\)、熱量を \(Q \, \mathrm{[cal]}\) で表すときには換算率 \(J\) が必要になるが、両者を共通の単位 \(\mathrm{[J]}\) で表すことににすれば、この換算率 \(J\) は不要になる。また \(\Delta U = U_2 – U_1\) とすれば、式\(\text{(5.3.4-1)}\) は

$$ \Delta U = Q+W \tag{5.3.4-2} $$

と書くことができ、見慣れた式になる。ここで、

\begin{alignat}{3}
&U & \quad & \colon \; 内部エネルギー & \qquad \qquad \qquad & \mathrm{[J]} \\
&Q & \quad & \colon \; 外部から流入する熱量 & \qquad \qquad \qquad & \mathrm{[J]} \\
&W & \quad & \colon \; 外部からなされる仕事 & \qquad \qquad \qquad & \mathrm{[J]} \\
\end{alignat}

である。

ところで、\(U\) にのみ \(\Delta\) を付けている点に注目してほしい。熱力学で用いる \(\Delta\) は、状態量の変化量を意味している。すなわち、状態量ではない \(Q,W\) は、その変化量は一意に定まらず経路によって様々な値をとるから、変化量を定義できない。したがって、これらには \(\Delta\) を付けるべきではない。（状態量の説明は後述する）

式\(\text{(5.3.4-2)}\) の微分形は以下のようになる。

$$ \mathrm{d} U = \mathrm{d}^\prime Q + \mathrm{d}^\prime W \tag{5.3.4-3} $$

微分形においても、熱力学では状態量と非状態量を区別するために、非状態量に対しては \(\mathrm{d}^\prime\) を用いて全微分を意味する \(\mathrm{d}\) とは表記を分けることが多い。

5.3.5 内部エネルギーの性質

5.3.3節にて、内部エネルギーの概念を説明し、5.3.4節にて、熱力学第1法則としてこれを内包した。一方で、ここまでの議論では、内部エネルギーが体積や温度などのどのような関数であるかについては全くの未知である。当時の人たちにとっても謎に包まれており、いくつかの興味深い実験が実施された。とりわけ重要なのは、「理想気体の内部エネルギーは温度のみに依存する」という結論である。これは、経験事実である。後に、気体分子運動論（その後統計力学へと発展する）にて同様の結論を得るが、古典熱力学ではそのようなミクロな視点は持っておらず、マクロな視点において構築された学問体系であることに注意されたい。なお、理想気体の状態方程式 \(pV=nRT\) を用いても、同じ結論を得るが、温度の定義を厳密にしないと状態方程式は意味をなさないので、状態方程式を前提にしてはならない。（後述）

この実験として有名なのは、ジュールが1845年に実施した「自由膨張の実験」である（図5.3.5-1）。

ジュールは1845年にこのことを調べるために次のような実験を行った。すなわち、図5.3.3-1のように、Aに約22気圧に圧縮した空気を入れ、Bは はじめ真空にしておいて、栓Cをもつパイプで連結し、全体を外部と熱の出入りの全くない水中に置いた。そこで栓CをあけるとAの中の気体がBの中に広がるから体積は膨張する。しかしこの場合には、気体分子は真空中に広がるので、物に当たってこれを押し動かすのではないから、外部に仕事をしない。このような膨張を自由膨張という。

2つの容器内の気体が温度平衡に達するまで待っていると、2つの容器内の気体の温度は最初のAにあった気体の温度と同じになった。つまり、膨張前後では温度変化のないことを認めた。このときの条件を考えると、容器内の気体は膨張前後において外部から仕事も熱も受け取っていないから、式\(\text{(5.3.4-2)}\) において \(Q = 0, W = 0\) である。したがって \(U_1 = U_2\) となる。すなわち、内部エネルギーと温度は不変であって体積が増加したことになる。言いかえると、内部エネルギーを体積と温度の関数と考えれば、体積に無関係で温度 \(T\) だけの関数ということができる。式で書けば

$$ \left( \frac{\partial U}{\partial V} \right)_T = 0 \tag{5.3.5-1} $$

となる。これをジュールの法則とよんでいる．

関連文書（1）より抜粋。ただし、式番号等は本記事に合わせて変更した。

気体温度の計測について、実際には水槽の温度を計測している。すなわち、容器全体を水槽に浸けて、熱平衡となったときの水槽の水温をまず測定しておく。その後、栓Cを開いて熱平衡となったとき水槽の温度が変化するかどうかを確かめたのである。また、式\(\text{(5.3.5-1)}\) の添え字 \(T\) は一定ということを意味する。

この実験を要約すると、次のようになるだろう。
「気体の内部エネルギー \(U\) を一定として体積 \(V\) を変化させても（当然 圧力 \(p\) も変化する）、温度 \(T\) は変化しない。」

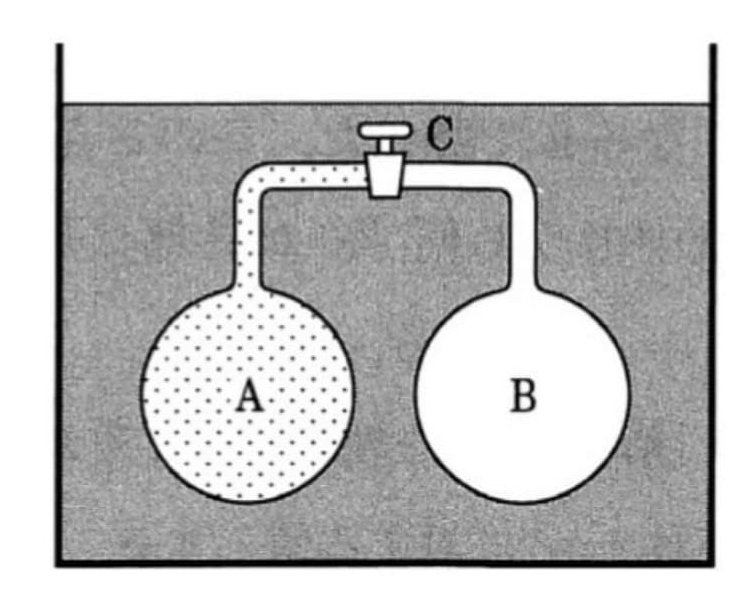
図5.3.3-1：自由膨張の実験
（関連文書（1）より抜粋）

これは、謎に満ちた内部エネルギーの性質の一部を明らかにした、非常に重要な実験である。以下に示すように、関連文書（2）でも力説されているが、「理想気体の内部エネルギーは温度のみに関係し体積や圧力には無関係である」という結論は、経験事実に基づいている。

この経験的な事実から「理想気体の内部エネルギーは温度のみに関係し体積や圧力には無関係です。」という重要な結論が得られる。これは最初 ”マイヤーの仮説” と言われていたが、今日では ”ゲーリュサック=ジュールの法則” と呼ばれている。

これは状態方程式からは決して得られない、理想気体について一歩踏み込んだ性質です。状態方程式は \(p\) と \(V\) と \(T\) が互いにどの様に関係して変化するかを示しているだけで、状態が決まったとき（つまり \(p,V,T\) が決まったとき）の内部エネルギーがどういった値になるのかは何も教えてくれない。その何も解らない内部エネルギーについて一歩踏み込んだ性質を教えてくれています。ただし内部エネルギーが温度にどの様に関係するのかは何も教えてくれない。

関連文書（2）より抜粋

もっとも、理想気体の状態方程式 \(pV=nRT\) を認めると、数式的に上記の結論を示すことができるが、状態方程式は温度の定義を完全にしないと意味を持たないから、これを前提に考えるべきではない。

例えば水の融点を0℃、沸点を100℃として、ある物質の体積膨張を読み取り、0℃～100℃の膨張量を100等分して温度目盛りを作ることができる。物質を変えると、0℃と100℃は合わせることができるが、中間温度帯では一般に目盛りが一致しない。これは、体積膨張率が温度依存するために、温度に対して一定の膨張率を示さないためである。したがって、厳密な温度というときには、どの温度計で測ったかを明示しなければ意味を持たない。このように、実在の物質を用いた温度計は不便なので、実在の物質によらない合理的な温度目盛りを決定できるか、は大いなる疑問であった。今日、熱力学第2法則を使うと、もっとも合理的に温度を定義できることが知られている。ただし、理論的に決まるのは温度の比であって、目盛の単位は別に定めなくてはならない。これを絶対温度または熱力学温度という。

一方で、ジュールの行った上記の実験には、次のような欠点があり、さらなる改良を施した実験が行われた。

ジュールの行ったこの実験装置では、気体の熱容量が容器やその他の器具の熱容量に比べて非常に小さいから、温度が少しくらい変化してもそれを認めることができない。さらに精密に行ったのが、通常 ジュール＝トムソンの細孔栓の実験とよばれるジュールとトムソンの共同実験である（1861年）。

この実験は図5.3.5-2 のように、外部から熱の出入りを完全に遮断できる壁（断熱壁という）で作った管の一部に綿その他の多孔性の物質を詰めた細孔栓（図中のC) を置き、AC間に一定量の気体を入れ、圧力を一定に保ちながらピストンAをゆっくりと押していくと、多孔質の栓を通過するとき圧力が低下してCB間に流れていく。ピストンを連続的にはたらかせて、管内の気体の移動が定常的になるようにして、 A側とB側の圧力 \(p_\mathrm{A}, p_\mathrm{B}\) \((p_\mathrm{A}>p_\mathrm{B})\) および温度 \(T_\mathrm{A}, T_\mathrm{B}\) を測定する。

多孔質の栓を通過することにより気体の状態がどのように変化するかを考えるに、AB間の気体部分がA’B’間に進んだとすると、結果としてはAA’間の気体がBB’間に移ったのと同等である。いま、AA’間およびBB’間の体積を \(V_\mathrm{A}, V_\mathrm{B}\) とすれば、このとき外力が気体にした仕事は \(p_\mathrm{A} V_\mathrm{A}\) であり、気体が外部に対してした仕事は \(p_\mathrm{B} V_\mathrm{B}\) である。したがって、正味気体が外部からされた仕事 \(W\) は

$$ W = p_\mathrm{A} V_\mathrm{A} – p_\mathrm{B} V_\mathrm{B} \tag{5.3.5-2} $$

である。そしてこの間に外部からの熱の出入りはないから \(Q = 0\)、したがって第1 法則によって、この仕事はこの間における気体の内部エネルギーの増加 \(U_\mathrm{B}-U_\mathrm{A}\) に等しい。ゆえに

$$ U_\mathrm{B} -U_\mathrm{A} = p_\mathrm{A} V_\mathrm{A} – p_\mathrm{B} V_\mathrm{B} \tag{5.3.5-3} $$

または

$$ U_\mathrm{A} + p_\mathrm{A} V_\mathrm{A} ＝U_\mathrm{B} + p_\mathrm{B} V_\mathrm{B} \tag{5.3.5-4} $$

となる。この関係は細孔栓の実験において \(p_\mathrm{A},p_\mathrm{B}\) の値によらず成り立つのであるから

$$ U+pV=\mathrm{const.}=H \tag{5.3.5-5} $$

とおくことができる。

関連文書（1）より抜粋。ただし、式番号等は本記事に合わせて変更した。

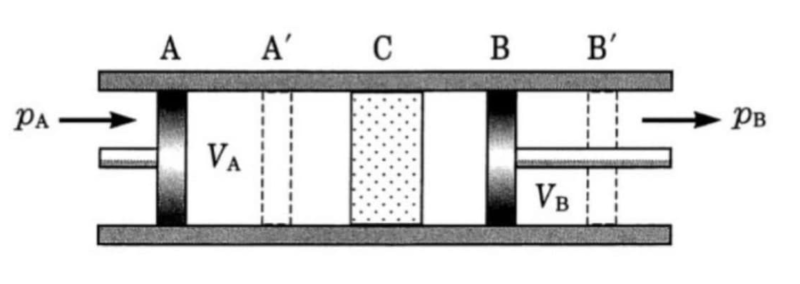
図5.3.5-2：ジュール＝トムソンの細孔栓の実験
（関連文書（1）より抜粋）

一般に、\(U + pV = H\) はギプスの熱関数またはエンタルピーとよばれている。\(U\) および \(pV\) が状態量であるので、\(H\) も状態量である。
ジュール=トムソンの実験は、エンタルピー \(H\) を一定という条件の下で気体を変化させるとき、その圧力変化 \(p_\mathrm{A}-p_\mathrm{B}=\Delta p\) に対する温度変化 \(T_\mathrm{A}-T_\mathrm{B}=\Delta T\) を調べる実験である。
実際の測定によると、室温、1気圧の付近では、多くの気体の \(\Delta T\) は正になる。つまり温度が下がる。たとえば炭酸ガスは室温で \(\Delta p=1\) 気圧のもとで行うと \(\Delta T\) は約1 K、空気では約0.2 K である。温度を低くして行うと温度降下は大きくなる。たとえば炭酸ガスでは -53 ℃で実験すると、\(\Delta p=1\) 気圧で、\(\Delta T\) = 2.3 K 降下する。しかし水素とヘリウムは室温付近で実験すると温度が上昇する。それを低温（水素では -80 ℃以下）で行うと降下するようになる。また、どんな気体でも密度が小さくなるとこの温度変化は小さくなることが示されている。このような温度変化をジュール＝トムソン効果という。

密度の小さい気体、つまり理想気体に近い気体の温度変化は小さいから \(\Delta T=0\) とすると、このときの仕事はボイルの法則にしたがうから \(p_\mathrm{A} V_\mathrm{A}=p_\mathrm{B} V_\mathrm{B}\) となる。したがって、式\(\text{(5.3.5-3)}\) の右辺はゼロとなるから

$$ U_\mathrm{A}=U_\mathrm{B} \tag{(5.3.5-6)} $$

となり、気体の内部エネルギーの変化がなく、また内部エネルギーが体積に関係しないことを意味している。これは前述のジュールが単独に行った実験の結果と一致する。このように考えると、ジュール＝トムソンの実験は実在気体の理想気体からのずれを示す実験といえる。また、式\(\text{(5.3.5-1)}\) で示されるジュールの法則は理想気体の特性であるともいえる。

関連文書（1）より抜粋。ただし、式番号等は本記事に合わせて変更した。

ここで、ボイルの法則を以下に示す。

そもそも気体についての研究は、ゲーリケによって真空ポンプが発明されたために飛躍的に発展した。これを知ったボイルは種々の気体について実験し、一定量の気体の温度を一定に保っておけば、その圧力と体積との積は一定になることを見出した（1662 年）。圧力を \(p\)、体積を \(V\) として式に書き表すと

$$pV=\mathrm{const.} \tag{5.3.5-7} $$

となる。ただし、この定数は気体の種類と質量および温度によって異なった値をとる。この関係は液化しがたい気体、たとえば水素、酸素、空気、窒素またはネオン等の希ガスでは相当正確に成立する。しかし厳密にいうと、圧力が増大（密度が増大）してくると式\(\text{(5.3.5-7)}\) は成り立たなくなる。一般にボイルの法則が成立するのは密度が小さい場合である。

関連文書（1）より抜粋。ただし、式番号等は本記事に合わせて変更した。

ジュール＝トムソンの細孔栓の実験を要約すると、次のようになるだろう。
「エンタルピー \(H=U+pV\) を一定にして体積 \(V\) を変化させると（当然 圧力 \(p\) も変化する）、実在気体では細孔栓の通過前後で多少の温度変化が見られたが、いずれの気体においても密度が小さくなると温度変化は小さくなった。よって、温度変化がゼロとなるような仮想的な気体を理想気体と呼ぶことにした。すると、理想気体においては、この実験では内部エネルギー\(U\) は変化せず、温度 \(T\) も変化しないとしてよいだろう。つまり、理想気体の内部エネルギーは温度のみに関係して体積には無関係（圧力にも無関係）である。」

高校物理では、理想気体の状態方程式 \(pV=nRT\) が最初にでてきて、これありきで議論が進められることが多いが、状態方程式と熱力学の関係を以下に示す。

熱力学に関する書物を開くと、必ずといってよいくらい状態方程式が顔を出す。状態方程式はあとで学ぶ熱力学の法則から出てくる性質のものではない。それは経験的に個々の対象について定められると考えるべきものである。

（中略）熱力学はもともとこれらの状態方程式も考慮して、これらに矛盾しないように組み立てられたものである。したがって、状態方程式と熱力学はそれぞれ独立に存在して、しかも両者を組合わせて利用できるものである。

関連文書（1）より抜粋

すなわち、熱力学からは状態方程式を導くことができない。では、上記に示したジュールの実験結果やジュール＝トムソンの実験結果と、状態方程式の関係はどうなるかというと、実在物質を用いた温度計（絶対温度でなくてもよい）で、ジュールの実験やジュール＝トムソンの実験を行い、理想気体の内部エネルギーは温度のみに関係して体積には無関係（圧力にも無関係）であることを示す。そして、後に、絶対温度 \(T\) を厳密に定義できたならば、状態方程式の温度を絶対温度で表記すると、これらの実験結果と矛盾しない、ということである。この辺の解説は、関連文書（2）が詳しい。

5.3.6 状態量

状態量の説明を、関連文書（1）より抜粋する。

ある系が熱力学的平衡状態になれば、その状態に達する経路には関係なく、その系に特有な値として定まるような物理量を状態量という。

状態量の概念は次のような日常生活について考えると一層はっきりするであろう。

われわれの日常生活では道筋によるものと、道筋によらない2種の違った量が存在する。この2つの区別は、ある町から山の中腹当りにある山の町まで、自動車で行くことを考えると容易に理解できる。すなわち、この2つの町の間には3 本の異なった道路があったとする（自動車で芦の湖へ行くことを考えよ）。いま、一方の町から出発して、山腹の道路を上下したりして他の町に到着すると、上がった高さは結局、 このドライブの終りの町と出発した町の高度の差である。同じ出発点、到着点に対して、全く違った道を通ったとしても、登りの正味の高さは同じで、出発点と到着点の高さの差だけで決まる。これは道筋によらない典型的な例である。

一方、2つの町の間の距離を測るのに、自動車の距離計を使えば、これは道筋によって大変違う。どの道を通ったかによって走行キロ数は変ってくる。したがって、走行距離は道筋による量である。前者を状態量とよび、後者は状態量になることができないので、これを非状態量とよぶのである。

（中略）状態量、非状態量の定義は以上のようであるが、数学的表現をとるとき、この両者の差は一層明瞭になる。すなわち、状態量は数学的には全微分となる。これに反して非状態量は全微分にならない。逆に、ある関数が全微分になっていればその関数は状態量である。

関連文書（1）より抜粋

ある平衡状態に対して一意に定まるような値を状態量という。したがって、始まりと終わりの状態が決まれば、その変化量も一意に定まる。これはかなり便利である。例えば5.2節では、この性質を利用してシンプルに解答している。すなわち、内部エネルギーの変化量は経路によらないから、計算が楽な定積変化を考えて \(\Delta U\) を算出したが、得られた結果は定積変化に限定されるものではない、ということだった。

全微分について簡単に紹介する。
いま、2変数関数 \(z=f(x,y)\) を考える。ある位置 \((x,y)\) から微小変化した位置 \((x+\mathrm{d} x, y+\mathrm{d} y)\) における \(z\) の微小変化 \(\mathrm{d}z\)は、

$$ \mathrm{d}z = \frac{\partial f}{\partial x} \mathrm{d}x + \frac{\partial f}{\partial y} \mathrm{d}y \tag{5.3.6-1}$$

と表すことにする。このとき、\(\mathrm{d}z\) を \(f\) の全微分という。なお、このように \(\mathrm{d} z\) が表現されるとき、その積分値は経路によらず、始点と終点のみに依存する。すなわち、ある点AからBへの \(z\) の変化量は、

\begin{align}
\begin{split}
\int_{A}^{B} \mathrm{d}z &= z(B) – z(A) \\[0.5em]
&= f(x_B, y_B) – f(x_A, y_A)
\end{split}
\tag{5.3.6-2}
\end{align}

となる。
より一般的には、次の微分方程式

$$ \mathrm{d} z = P(x,y) \mathrm{d} x + Q(x,y) \mathrm{d} y \tag{5.3.6-3} $$

があったとする。このとき、\(\mathrm{d}z\) が全微分であるための必要十分条件は、

$$ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} \tag{5.3.6-4} $$

である。すなわち、

\begin{align}
\begin{split}
\frac{\partial f}{\partial x} = P \\[0.5em]
\frac{\partial f}{\partial y} = Q
\end{split}
\tag{5.3.6-5}
\end{align}

なる関数 \(z=f(x,y)\) の存在が保証され、これが状態量に他ならない。

例として、仕事 \(W\) が状態量でないことを、数学的に示す。

準静的過程においては、微小な仕事は次のように表すことができる。

$$ \mathrm{d}^\prime W = -p\mathrm{d} V \tag{5.3.6-6} $$

つまり、仕事 \(W\) は \(p, V\) の関数と考えることができるので、

$$ \mathrm{d}W = \frac{\partial f}{\partial p} \mathrm{d}p + \frac{\partial f}{\partial V} \mathrm{d}V \tag{5.3.6-7} $$

を満たすような関数 \(W=f(p,V)\) が存在すると仮定する。式\(\text{(5.3.6-6)}\) は変形すると

$$ \mathrm{d}^\prime W = 0 \cdot \mathrm{d}p {}- p \mathrm{d} V \tag{5.3.6-8} $$

となるから、式\(\text{(5.3.6-7)}\) および 式\(\text{(5.3.6-8)}\) から、

\begin{align}
\begin{split}
\frac{\partial f}{\partial p} &= 0 \\[0.5em]
\frac{\partial f}{\partial V} &= -p
\end{split}
\tag{5.3.6-9}
\end{align}

が成り立たねばならない。一方、全微分であることの必要十分条件より、

$$ \frac{\partial}{\partial V} \left( \frac{\partial f}{\partial p} \right) = \frac{\partial}{\partial p} \left( \frac{\partial f}{\partial V} \right) \tag{5.3.6-10} $$

も成り立たなければならない。しかし、

\begin{align}
\begin{split}
\frac{\partial}{\partial V} \left( \frac{\partial f}{\partial p} \right) &= 0 \\[0.5em]
\frac{\partial}{\partial p} \left( \frac{\partial f}{\partial V} \right) &= -1
\end{split}
\tag{5.3.6-11}
\end{align}

となるから、式\(\text{(5.3.6-10)}\) は成り立たない。すなわち、最初の仮定が誤りであり、仕事 \(W\) は全微分で表現できないことから、状態量ではない。

5.3.7 最終的な解答

かなり長くなったが、ここまでくれば 5.2節に示した解答とほとんど同じである。
5.3.1節に示した、再整理した問題文を再記する。

理想気体において、ある平衡状態から温度が \(\Delta T \, \mathrm{[K]}\) 変化して別の平衡状態となったとき、内部エネルギーの変化量は \(\Delta U = n C_V \Delta T\) と表せることを示せ。なお、理想気体の物質量を \(n \, \mathrm{[mol]}\) 、定積モル比熱を \(C_V \, \mathrm{[J/(mol \cdot K)]}\) とする。

5.3.5節より、理想気体の内部エネルギーは温度のみに依存する。よって、計算が楽な定積変化で考えると、仕事 \(W=0\) であるから、熱力学第1法則（式\(\text{(5.3.4-2)}\)） より、\(\Delta U = Q\) となる。一方、定積モル比熱の定義から、定積変化における \(Q = n C_V \Delta T\) であるから、内部エネルギーの変化は、\(\Delta U = n C_V \Delta T\) と表せる。（解答終わり）

6. おわりに

結局、問題を解くのに使った法則は、

• 熱力学第1法則
• 理想気体の内部エネルギーは温度のみに依存する

たった2つであることに注意いただきたい。分子がどうとか言わなくてもよいし、理想気体の状態方程式すら不要である。

一方で、題意は、平衡状態が決まればその過程に全く依存しないという、とてつもなく広い範囲へ適用できることは注目に値する。