1. 概要
工学的に広く使用される温度計として、熱電対(ねつでんつい)がある。簡便な使用方法で低温から高温まで幅広い温度計測を行うことができる。一方で、その原理詳細を記した情報がweb上に少なかったので、本記事では熱電対の原理を示す。
2. 関連文書
本記事に関する関連文書を下表に示すが、本記事の内容は主に関連文書(1)~(5)を参考に記述している。
3. 熱電対の原理
ある金属棒の一端を加熱した場合、他端へ熱伝導による熱伝達が生じることは日常でもよく体験する現象である。実はこの時、熱以外にも金属内部の自由電子が移動している。もちろん、回路としては開いているので電流は流れないが、端部は帯電し、熱起電力 \(E_{\alpha\beta}\) が発生する。
図3-1:材質Aに温度勾配を付けた場合の様子
熱起電力 \(E\) の正負や大きさは材質によって様々であるが、温度差1Kあたり約±1~100μVの小さな値であり、この1Kあたりの熱起電力をゼーベック係数(\(S\))または熱電能という。ただし、右辺の負号に注意。
$$ S=-\frac{\Delta E}{\Delta T} \tag{3-1} $$
とくに、単体物質のものであることを強調する場合には、絶対ゼーベック係数または絶対熱電能という。また、絶対ゼーベック係数は物質固有の値であり、導体の長さや太さなどの形状によらず、その材質と温度のみに依存する。すなわち、材質 \(\mathrm{A}\) の絶対ゼーベック係数を \(S_\mathrm{A}\) と表すことにすると、
$$ E_{\alpha\beta}=E_\beta-E_\alpha= \int^{T_\beta}_{T_\alpha} -S_\mathrm{A} \, \mathrm{d}T \tag{3-2} $$
と表せる。一般に、ゼーベック係数 \(S\) は温度に依存するため、積分の外に出すことはできない。
では、次のように温度分布を与えた場合、開放端の熱起電力 \(E_{13}\) はどうなるだろうか。
図3-2:材質Aに温度勾配を付けた場合の様子(その2)
\begin{align}
\begin{split}
E_{13}&=E_{12}+E_{23} \\
&= \int^{T_2}_{T_1} -S_\mathrm{A} \, \mathrm{d}T+\int^{T_1}_{T_2} -S_\mathrm{A} \, \mathrm{d}T \\
&= \int^{T_2}_{T_1} (S_\mathrm{A}-S_\mathrm{A}) \, \mathrm{d}T \\
&= 0
\end{split}
\tag{3-3}
\end{align}
となり、開放端における熱起電力はゼロとなる。上側と下側で熱起電力の大きさが等しく向きが逆のため、打ち消しあってしまうのだ。すなわち、均質な材質で構成される回路の場合、その熱起電力はゼロとなる。\(T_1\) を計測機側の端子、\(T_2\) を測温部として使いたいが、これでは \(T_2\) が如何なる温度であっても、計測機側の電圧はゼロとなるため、無意味な計測となってしまう。
次に、2種類の材質を接合してみよう。
図3-3:材質AおよびBに温度勾配を付けた場合
\begin{align}
\begin{split}
E_{13}&=E_{12}+E_{23} \\
&= \int^{T_2}_{T_1} -S_\mathrm{B} \, \mathrm{d}T+\int^{T_1}_{T_2} -S_\mathrm{A} \, \mathrm{d}T \\
&= \int^{T_2}_{T_1} (S_\mathrm{A}-S_\mathrm{B}) \, \mathrm{d}T
\end{split}
\tag{3-4}
\end{align}
2種類の材質を用いたことで、絶対ゼーベック係数の差異が \(E_{13}\) として現れるようになる。したがって、\(T_1\) をある適当な温度に固定して \(T_2\) を変化させた場合の \(E_{13}\) を取得して \( T_2 \, \mathrm{vs}. E_{13} \) の一覧表を作っておけば、計測時は同じ \(T_1\) を再現する必要はあるが、\(E_{13}\) を計測し前述の一覧表と照らし合わせることで、未知の\(T_2\) を決定できる。 これが、熱電対の原理である。
今日、実用的に用いられる材質 \(\mathrm{A/B}\) の組み合わせはいくつかあり、測定温度範囲によって使い分ける。また、通常 \(T_1\) は0℃とする。日本工業規格(JIS)においても、\(T_1\) を0℃とした「規準熱起電力表」が熱電対の種類毎に示されている。(関連文書2(6))
上記の熱電対の原理を忠実に実行する試験系は以下のようなものである。
\(T_1\) を0℃にするには、その部分を氷水に浸漬させればよく、比較的容易に実現できる。
電圧計測について、前述では理想的な計測を示したが、実際には電圧計まで導線で接続する必要があるし、電圧計の内部も0℃に維持することは困難である。したがって、新たな材質 \(\mathrm{C}\) と温度 \(T_3\) が追加される。すなわち、新たに熱電対 \(\mathrm{C/A}\) および \(\mathrm{C/B}\) が形成されてしまう。
図3-4:計測系の例
なんだかややこしくなってきたが、電圧計で計測される電位差 \(E_{04}\) を計算してみよう。
$$ E_{04}=E_{01}+E_{12}+E_{23}+E_{34} \tag{3-5} $$
ここで、図3-2で示したように、均質な材質で構成される回路の場合、その熱起電力はゼロとなるので、
$$ E_{01}+E_{34}=0 \tag{3-6} $$
式(3-6)を式(3-5)に代入すると、
$$ E_{04}=E_{12}+E_{23} \tag{3-7} $$
さらに、式(3-4)より、
$$ E_{04} = \int^{T_2}_{T_1} (S_\mathrm{A}-S_\mathrm{B}) \, \mathrm{d}T \tag{3-8} $$
となる。すなわち、材質 \(\mathrm{C}\) や \(T_3\) に関係なく、電圧計における計測値は図3-3と同じ \(E_{13}\) になるのである。
一方で、\(T_1\) を0℃に維持することは、長期間の計測や、計測場所によっては実施困難なことがある。そのため、熱電対を扱う汎用データロガーでは、冷接点補償を行い、\(T_1\) を0℃に維持しなくてよい方法を採用している。まず、熱電対の性質「中間温度の法則」を説明する。
図3-5に示すように、\(T_1\)~\(T_2\) までの熱電対1と、\(T_2\)~\(T_3\) までの熱電対2、\(T_1\)~\(T_3\) までの熱電対3の3本を考える。このとき、それぞれの熱電対の開放端における電位差を比較すると、以下の関係が成り立つ。
$$ E_1+E_2=E_3 \tag{3-9} $$
これを中間温度の法則というが、ゼーベック係数は導体の長さや太さなどの形状によらず、その材質と温度のみに依存する、という性質を考えれば当然の法則である。
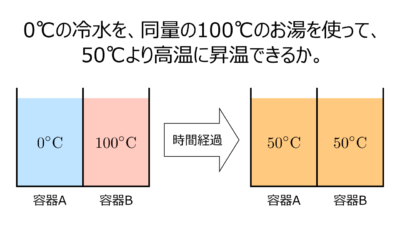
ただし、勘違いしやすいのは、例えば \(T_1=0 ^\circ \mathrm{C} \)、\(T_2=50 ^\circ \mathrm{C} \)、\(T_3=100 ^\circ \mathrm{C} \)のとき、\(E_1 \neq E_2 \) である。温度幅は同じ \(50 ^\circ \mathrm{C}\)だが、ゼーベック係数は温度に依存するため、それぞれの熱起電力は等しくない。もちろん、その合計値は \(E_3\) に等しい。
図3-5:中間温度の法則
中間温度の法則を利用すると、図3-4における \(T_1\) を0℃に固定しなくてよいことが分かる。すなわち、\(T_1\)が既知であれば、次のように \(T_2\) を求めることができる。
ある温度 \(T_\alpha \) からある温度 \(T_\beta \) までの熱起電力(@材質 \(\mathrm{A/B}\) の熱電対)を \(E_{T_\alpha \rightarrow T_\beta} \) と表すことにすると、知りたいのは \( E_{0 ^\circ\mathrm{C} \rightarrow T_2} \) である。これが分かれば、材質 \(\mathrm{A/B}\) の熱電対に対する規準熱起電力表から\(T_2\) を決定できる。中間温度の法則より、
$$ E_{0 ^\circ\mathrm{C} \rightarrow T_2}=E_{0 ^\circ\mathrm{C} \rightarrow T_1}+E_{T_1 \rightarrow T_2} \tag{3-10} $$
ここで、\(E_{0 \rightarrow T_1}\)は、今 \(T_1\) は既知としたので、規準熱起電力表から計算できる。また、\(E_{T_1 \rightarrow T_2}\) は電圧計の計測値そのものである。したがって、\(E_{0 \rightarrow T_2}\) を求めることができる。汎用データロガーでは、このように \(E_{0 \rightarrow T_2}\) を算出し、温度表示を行っている。
なお、汎用データロガーでは、端子部となる基板近傍の温度をサーミスタ等により計測し、\(T_1\) としていることが多い。
上記から分かるように、データロガーの接続部温度 \(T_1\) は \(T_2\) の算出精度に影響を与えるため、データロガー本体は温度の安定した場所に設置することが望ましい。
図3-6:計測系の例 (冷接点補償)