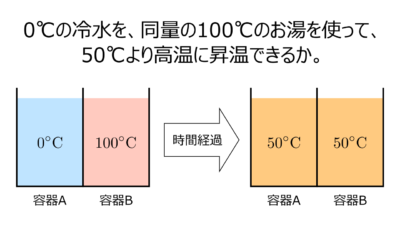
1. 概要
2022年1月15(土)~16(日)に、大学入学共通テストが実施された。従来のセンター試験に相当するものである。今回、その中でも数学ⅠAの難化が凄まじく、平均点の低下も相まって伝説になったという。俺もかつては数学が得意な高校生、解いてやろうではないか、と意気込んだものの、なんと得点は20点(100点満点中)であった。
問題の解説はいろいろな場所でされているので、ここでは解説はせず、各問題への感想と、受験生時期から16年以上経過した男がどの問題にどのようにつまづいたかを、記録として残す。
俺がセンター試験を受けたのは2006年のことだったが、難関国公立を目指すならば、数学ⅠA・ⅡBは満点を取って当然の科目だった。ⅡBは計算量がエグいので、満点は無理でも9割以上は取らなければならなかった。それに比べてⅠAは、試験時間の半分ほどで解き終わるので、満点以外ありえない科目だったと思う。しかし、俺は数学ⅠA本番で大問1個をまるまる落とし、75点だった。この大問は確率の問題であり、以降、確率がトラウマになっている。あとから見ればなんてことはない問題だったのだが、当日は本当に解けなかったのである。たしかに、俺は確率が本質的に苦手だったが、未だに何故あの問題が解けなかったか、分からない。
その後の自己採点にて、センター試験の合計点数が志望校の足切りギリギリのラインとなってしまった。いろいろあって、志望校を変え、現役で他大学へ進学することとなった。もし、数学ⅠAで満点を取っていたら第一志望の二次試験を受けていただろうし、そうでなくても、浪人して再挑戦する道もあっただろう。どの道が一番良かったかなど、分かるはずもないのだから、あり得た可能性を考えることに意味はない。だが、今振り返ると、この数学ⅠAは、自分の人生の岐路だった。こんな岐路は後にも先にもこれしかない。
上記のように、俺はセンター試験にトラウマを抱えており、実際に受験したとき以外、自ら問題を解くなんてことは無かった。それが、2022年度の数学ⅠAがヤバい、と聞いて解かずにはいられなかったのである。
解く、と決めてから、当時のことが鮮明に思い出されてくるのであった。高校生という時期は、人生で一番勉強する時期である。おじさんになった今では数学ⅠAだけで四苦八苦しているのだが、当時は英語、物理、化学、現代文、古文、など信じられないくらい多くの科目をこなさなければならなかった。また、故郷で過ごした最後の年でもある。当時は気づくはずもないが、流れに身を任せて生きていくならば、この地に戻ることはたぶん無いのである。今では変わってしまった関係性や、亡くなってしまった人、そんなことに思いを巡らすきっかけとなった。
未だに、闘い終わった者に掛けるべき言葉を知らないのだが、
受験生の皆様、お疲れ様でした。世間では伝説などと言われていますが、本当の意味でこの問題の難しさや理不尽さを理解できるのは、リアルタイムでこれに挑んだ者だけです。人生はそれだけじゃない、これは真ですが、それは遠い未来に振り返るときの視点です。十数年も生きていない今を生きる者にとって、受験はそれまでの人生の多くの時間を掛けた学業の集大成をぶつけるなにかであり、自分の岐路となるであろう一大イベントです。多くを懸けてこの問題に臨まざるを得なかった、その挑戦者の一人であったことに敬意を表します。
当事者であるうちに気づくことは難しいが――― 結果はどうあれ、いつの日かこの日々を振り返ったときに、受験できる機会が、学業に集中できる環境が、与えられていたことに思いを馳せてほしい。
2. 詳細
2.1 第1問[1]

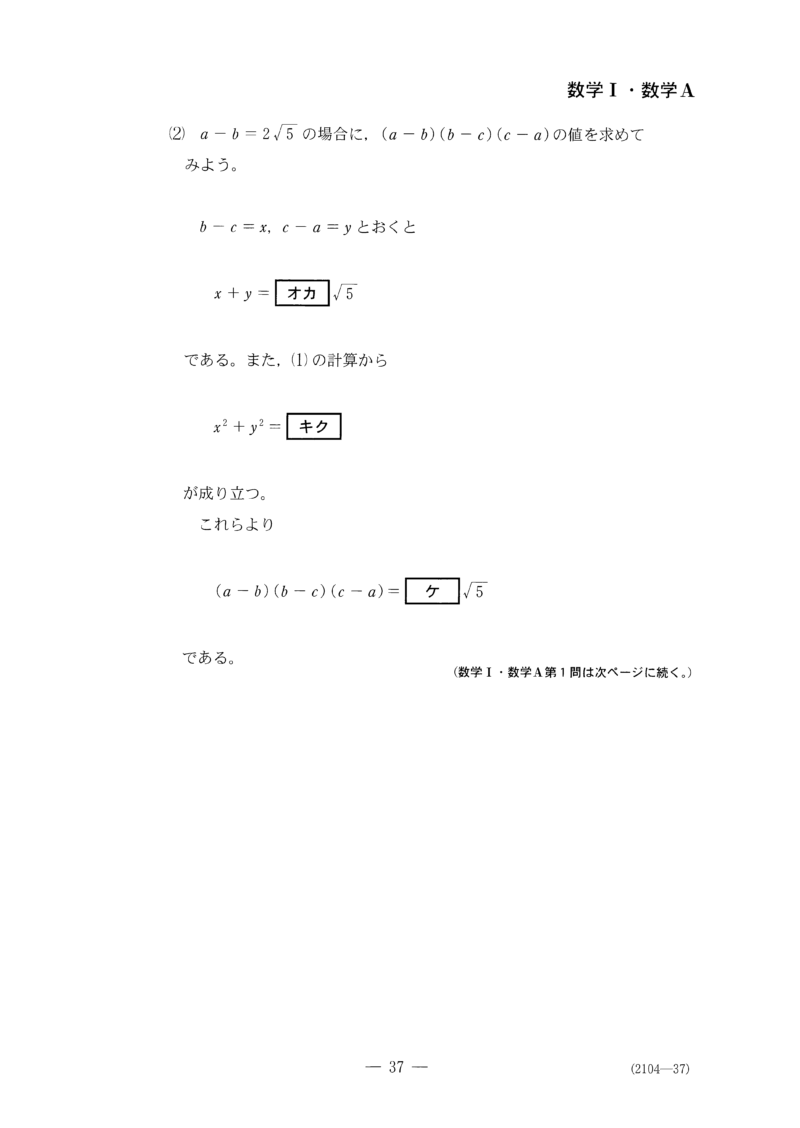
式展開に関する内容である。俺はまず、
$$ (a+b+c)^2 $$
の展開につまづいた。ごり押しで展開して解いたのだが、何かうまい方法はないのだろうか、と後で調べて辿り着いたのが、以下に示す多項定理である。
$$ (x_1+x_2+\cdots+x_m)^n $$
という式の展開式の一般項は、
$$ \frac{n!}{k_1! k_2! \cdots k_m!} x_1^{k_1} x_2^{k_2} \cdots x_m^{k_m} $$
と表せる。これを多項定理という。
\(x_1^{k_1} x_2^{k_2} \cdots x_m\) の項は、\(n\) 個の括弧のうちから \(x_1\) を \(k_1\) 個、\(x_2\) を \(k_2\) 個、\(\cdots\)、\(x_m\) を \(k_m\) 個選ぶ順列の総数なので、この項の係数は
$$ \frac{n!}{k_1! k_2! \cdots k_m!} $$
となる。
また、二項の場合、すなわち、
$$ (x_1+x_2)^n $$
に当てはめると、\(x_1^{k_1} x_2^{k_2}\) の項の係数は
\begin{align}
\begin{split}
\frac{n!}{k_1! k_2!} &= \frac{n!}{k_1! (n-k_1)!} \\[0.5em]
&= {}_n \mathrm{C}_{k_1}
\end{split}
\end{align}
となり、二項定理と一致する。
\(a+b\) の冪を
$$ (a+b)^n=\sum_{k=0}^n {}_n \mathrm{C}_k a^{n-k} b^k $$
の形の和に展開することができる。これを二項定理という。
今回の問題に当てはめると、括弧を2回かけるということは、2個の括弧うち \(a\) を \(p\) 個、\(b\) を \(q\) 個、\(c\) を \(r\) 個選ぶ順列の総数である。ただし、\(p+q+r=2\) である。だから、\(a^2\) の係数は
$$ \frac{2!}{2!0!0!}=1 $$
となる。また、対称式だから \(b^2, c^2\) の係数も\(1\) となる。同様に、\(ab\) の係数は、
$$ \frac{2!}{1!1!0!}=2 $$
となる。また、対称式だから \(bc, ca\) の係数も\(2\) となる。したがって、
$$ (a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca) $$
となる。
あとは難しいところは無いが、問題文が2ページにまたがって記載されているため、(2)の問題が大問[1]の中の2番目であり、(1)の内容も使うことに気付かないと詰む。ちなみに俺は、計算ミスにより大量失点&時間損失を犯してしまった。
2.2 第1問[2]
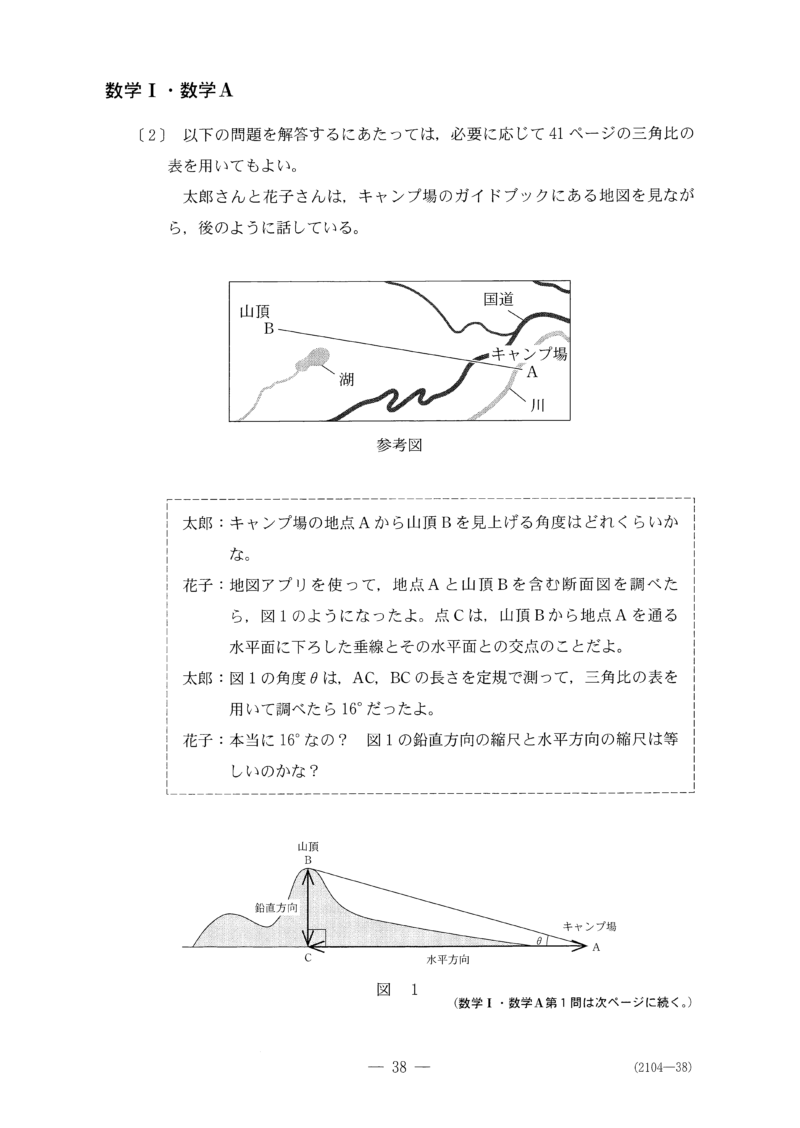

まず、太郎と花子の登場に驚く。現代文かな。問題文が長い割に中身は無い。三角比の根源的なところを突く問題だとは思うが、こんなことは大学入学共通テストで問われるべきではないだろう。3年間の勉強の末に問われる三角比の問題の一つがこれでいいわけがない。
2.3 第1問[3]
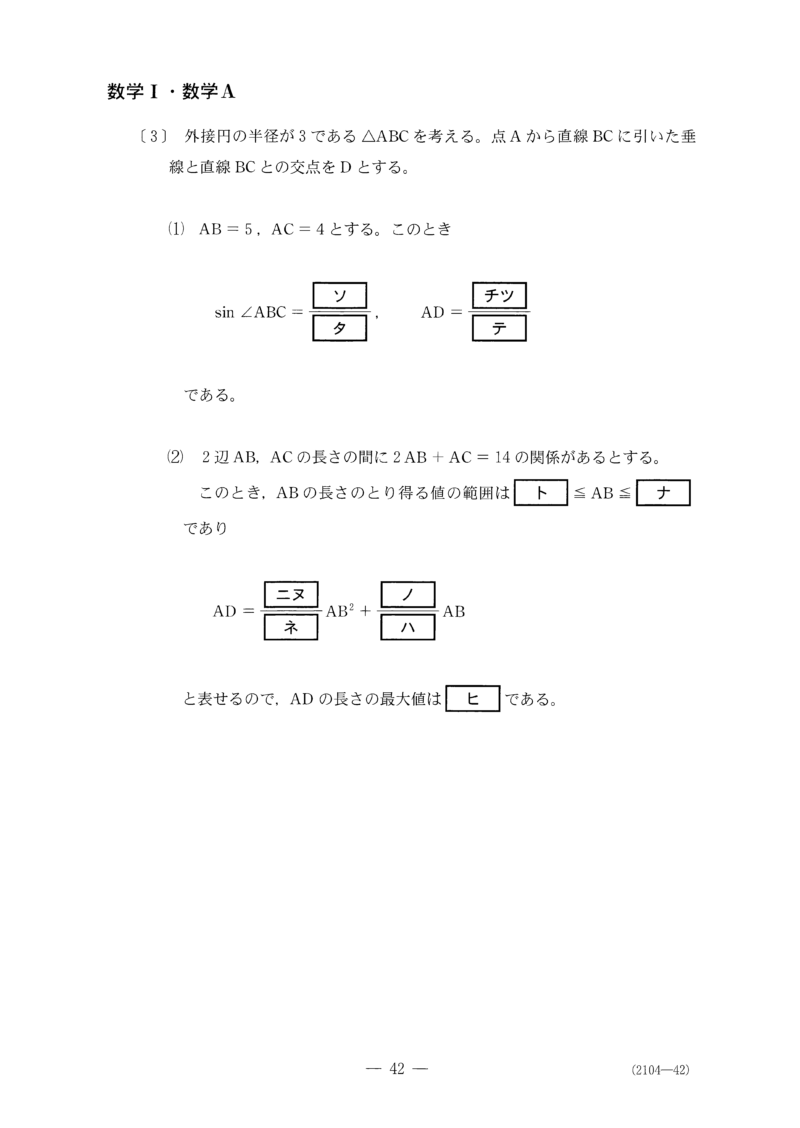
俺は正弦定理を完全に忘れていた。よってこの小問はゼロ点。
\(\triangle{\mathrm{ABC}}\) において \(\mathrm{BC}=a\)、\(\mathrm{CA}=b\)、\(\mathrm{AB}=c\)、外接円の半径を\(R\) とすると
$$ \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R $$
が成り立つ。これを正弦定理という。
証明は、下図を見れば分かると思う。
なお、円周角の定理については下図を参照のこと。
本問題では問われていないが、ついでに余弦定理も復習しておく。
\(\triangle{\mathrm{ABC}}\) において \(\mathrm{BC}=a\)、\(\mathrm{CA}=b\)、\(\mathrm{AB}=c\) とすると
\begin{align}
\begin{split}
a^2 &= b^2 + c^2 – 2bc \cos A \\[0.5em]
b^2 &= c^2 + a^2 – 2ca \cos B \\[0.5em]
c^2 &= a^2 + b^2 – 2ab \cos C
\end{split}
\end{align}
が成り立つ。これを余弦定理という。
証明は以下のようになる。
\(\mathrm{A}\) から \(\mathrm{BC}\) に垂線 \(\mathrm{BD}\) を引く。
直角三角形 \(\mathrm{ACD}\) に三平方の定理を用いると、
$$ \mathrm{AC}^2 = \mathrm{AD}^2 + \mathrm{CD}^2 $$
となる。これに、
\begin{align}
\begin{split}
\mathrm{AC} &= b \\[0.5em]
\mathrm{AD} &= c \sin B \\[0.5em]
\mathrm{CD} &= a – c \cos B
\end{split}
\end{align}
を代入すると、
\begin{align}
\begin{split}
b^2 &= (c \sin B)^2 + (a-c \cos B)^2 \\[0.5em]
&= c^2 (\sin^2 B + \cos^2 B) + a^2 -2ca \cos B \\[0.5em]
&= c^2 + a^2 -2ca \cos B
\end{split}
\end{align}
を得る。
正弦定理を覚えていれば、あとは難しいポイントは無い。
これでようやく第1問が終わる。しんどい。
2.4 第2問[1]



またしても太郎と花子の会話がでてくる。4ページに渡る問題となっているが、内容は薄い。しかし、読み間違いやすい文字による問題構成と、度重なる変数の変更、そして不要な会話と挿絵によるページ分断などにより、問題そのものの難易度よりも、短期記憶力や読解力に神経を割かなければならない。
(1)~(2)で太郎と花子の会話につきあって問いた末、(3)は単発の問題となる。一方(4)は、(1)~(2)を使う。(3)で意識を持っていかれているので、(1)~(2)で何を説いてたか忘れかかっている頃に(4)が待ち構えている。記憶力が試されている。
本来、数学の問題はシンプルでかつ短文であるべきである。そういう観点では、望ましい数学の問題ではない。読解力は現代文のほうで見てくれや。
2.5 第2問[2]




今回一番たまげた問題である。どうやら最近の数学ⅠAでは、現代文も範囲に入るらしい。
まず、俺の習った時代には、こんな内容は無いし、箱ひげ図など人生で聞いたことがない。後から調べてみると、「データの分析」という単元らしい。内容は、本当にデータ分析であり、特に数学と言えるものではない。標準偏差や分散といった考え方は重要だが、そこを教えるなら中心極限定理や正規分布と一緒にしないとあまり意味が無い (正規分布は数学Bで出てくるようである)。
2.6 第3問 (選択問題)

俺は確率にトラウマがあるので選択しなかった。しかし、この問題はかなり特殊で、いわゆる完全順列に関連するものである。初見で解ける人はどれくらいいるのだろうか・・・。
2.7 第4問 (選択問題)


今回の悪名高い設問の一つである。現代文というか、問題作成者の「独り言」であふれている。
昔も今も、俺は整数問題が苦手である。微分などの王道ツールは使えないし、解説を読んでも「そんな解法思いつくかよ」となる。それゆえ、整数問題(数論)は数学の究極の分野の一つであると思う。例えば素数に関わる問題や、20世紀に入り解決された Fermat’s Last Theorem もそうである。
今回の場合、式を満たす整数解を1つ見つけ、それを元の式から辺々引いて一般解を求める、という手法を使う。
\(5^4\) を \(2^4\) で割った余りが \(1\) だ、と独り言を垂れているから、\(x=1\) が解の一つである。このとき \(y=39\) である。
$$ 5^4 \cdot 1 {}- 2^4 \cdot 39 = 1$$
これを元の式から辺々引くと、
$$ 5^4(x-1) = 2^4(y-39) $$
を得る。ここで、\(5^4\) と \(2^4\) は互いに素であるから、\(k\) を整数として
\begin{align}
\begin{split}
x-1 &= 2^4 k \\[0.5em]
y-39 &= 5^4 k
\end{split}
\end{align}
でなければならない。このことから、\(x\) が2桁の正の整数で最小になるのは \(x=17\) だと分かる。
ここまではいい (俺は解けなかったが)。
問題なのは以下の独り言である。

何を言っているか分からないし、何を解こうとしていたのかも忘れたわ。誘導無視して解こうとするも、答えは5桁、絶望しかない。この独り言を理解できたとしても、次の(4)でまた付き合わなければならない。
2.8 第5問 (選択問題)
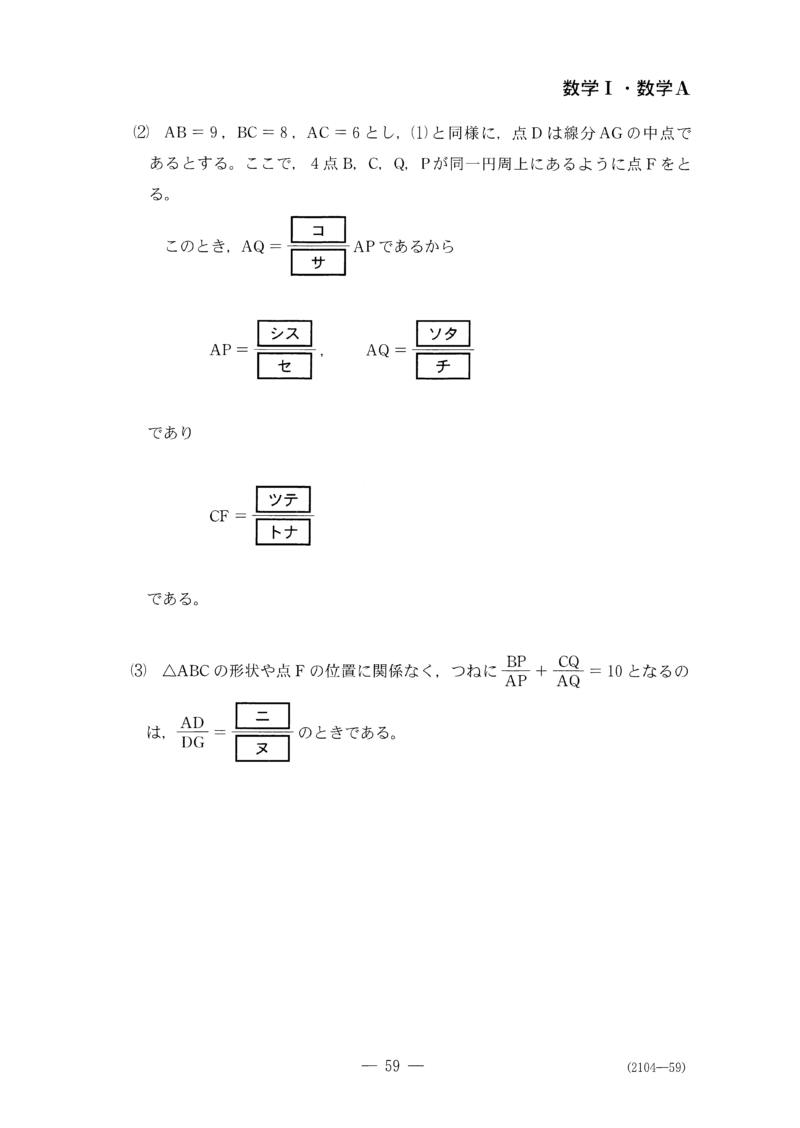
時間切れで全く手が出なかったが、時間があったとしても解けなかっただろう。
効率よく解くには、メネラウスの定理を使う。そんなもの、名前しか覚えていなかったが、相似則から導かれる定理の一つである。そんなものより、まず、三角形の重心の定義が怪しかった。これは自分としてもショックだった。
重心は物理でも重要なので、今一度復習する。
物体の各点に働く重力の合力の着力点を、重心という。
もっと直感的に言えば、物体を一点で支えられる位置のことをいう。一様な棒ならば長さの中心が、一様な円板ならば中心が、その物体の重心となる。ただし、重力が一様であれば、重心は重力の向きや大きさに関わらず、その物体の質量配分によってのみ決まる。そのため、質量の中心と考えてもよい。
では任意の三角形の重心はどこになるだろうか。
三角形の頂点と、その対辺の中点を結ぶ3つの線 (中線) は1点で交わり、その点は各中線を2:1に内分する。また、この交点は三角形の重心に等しい。
(ここでいう重心は、図心の意味であり、一様な密度を持つ薄板 (質量が板の面積に比例) の三角形を考えたときの重心である。しかし、上記の定義はしばしば、同質量の3つの質点が頂点A, B, Cにそれぞれあるだけの剛体としての重心として捉えられることもある。これは後で説明するが、物理的意味は全く異なるものの、三角形においてはどちらの意味の重心も同じ位置となる。)
いろいろでてきたが、まず中線が何故1点で交わるのか、について考えてみる。一見難しそうだが、実はこのことと、その交点が重心と一致することは直感的に理解できる。
下図のように、三角形を辺BCに平行な細い矩形の集合体であると考える。図の矩形幅は大きいが、これが気にならないように限りなく細い幅の矩形に分割していく。すると、それらの矩形の集合体は限りなく元の三角形に等しい (この限りなくという表現に違和感を覚える人はこの記事の3章の冒頭を参照のこと)。
矩形の重心は、明らかにその中点である。したがって、全ての矩形の重心は頂点Aから伸ばした中線上に存在する (図では代表して最下段と1個上の重心をそれぞれ赤〇、緑〇で示している) 。
さて、最下段と1個上の矩形を合体させると、合体させた重心は、あきらかにそれらの重心を結ぶ直線上に存在する。下段の方が面積が大きい (=質量が大きい) から、合体させた重心位置は、赤〇と緑〇の間の、やや赤〇寄りの位置になる。同様の操作を続けて、下から一段ずつ矩形を合体させていく。そのときの合体させた重心は、やはり頂点Aから伸ばした中線上に存在する。したがって、三角形ABCの重心は、頂点Aから伸ばした中線上に存在する。
上記の試行は、辺ABに平行な矩形としても、あるいは辺CAに平行な矩形としても同様の結果を得る。すなわち、三角形ABCの重心は、3本の中線上に存在する。したがって、3本の中線は1点で交わらざるをえないし、そこが重心となるのである。
中線の交点が重心となることは上記で分かったが、重心が中線を2:1に内分するのは何故か、を考えていく。これには、重心の位置を定量的に決定する方法を探らなければならない。
三角形は一度忘れて、両端に重りのついた棒を考える。棒の質量は考慮せず、両端の質量 \(m_1, m_2\) のみ考慮することとする。\(m_1=m_2\) ならば、重心の位置は明らかに棒の中点であるが、\(m_1 \neq m_2\) の場合は、重心の位置はどのように表せるだろうか。下図は、棒の重心を指で支えて静定した状態を示している。
棒の重心を実験的に求めていくと、任意の位置を支点として、力にその支点からの距離を乗じた値 (力のモーメント) がつり合うことに気が付く。すなわち、
$$ m_1 g x_1 + m_2 g x_2 = (m_1 + m_2)g x_\mathrm{G} $$
これを解くと
$$ x_\mathrm{G} = \frac{m_1 x_1 + m_2 x_2}{m_1 + m_2} $$
と求まる。すなわち、\(x_\mathrm{G}\) は、質量 \(m_1\) , \(m_2\) を重みとした加重平均になっていることが分かる。
今は2点だけで考えたが、質点の数を多くしても結果は同じであり、\(n\) 個の質点からなる質点群の重心は、
$$ x_\mathrm{G} = \frac{1}{M} \sum_{i=1}^n m_i x_i $$
と表せる。ここで \(M\) は全質量である。
$$ M = \sum_{i=1}^n m_i $$
例えば、3つの同じ質量の質点からなる質点群の重心は、
$$ x_\mathrm{G} = \frac{mx_1 + mx_2 + mx_3}{3m} = \frac{x_1 + x_2 + x_3}{3} $$
となる。これは、三角形の各頂点に質点があるだけの剛体の重心を意味している。(図心ではないことに注意を要するが、実は三角形に限っては図心も同じ座標となる。後述)
さて、実在の物体は連続体であり、上記のような質点で考えることは現実的ではない。このような場合、微小な要素について成り立つ式を考え、全体を記述する。すなわち、ある連続体の重心は
\begin{align}
\begin{split}
x_\mathrm{G} &= \lim_{\Delta m \to 0} \frac{1}{M} \sum_{i=1}^n x_i \Delta m \\[0.5em]
&= \frac{1}{M} \int x \, \mathrm{d}m
\end{split}
\end{align}
と表せる。
さて、三角形の重心に戻ろう。我々は、上記にて連続体の重心位置を計算する手段を得た。三角形の重心は中線上にあることは分かっているから、あとはその中線上の位置を計算で求められれば良い。これには、再び三角形を矩形に区切って考えていく。つまり、三角形の質量分布を高さ方向に1次元化することで、重心の高さを求めていく。
ある高さ \(y\) における幅 \(\mathrm{d}y\) の矩形を考える。三角形の相似より、
$$ w:h = l:h-y $$
となるから、
$$ l=\frac{w(h-y)}{h} $$
である。ここで、今、三角形は一様な密度を持つ薄板 (質量が板の面積に比例) で構成されているから、その面密度を \(\rho\)、全面積を \(S\) とすると
$$ M = \rho S = \frac{1}{2}\rho w h $$
となる。また、高さ方向 ( \(y\) 方向) の微小質量 \(\mathrm{d}m\) は矩形の質量であるから、
$$ \mathrm{d}m = \rho l \mathrm{d}y = \rho \frac{w(h-y)}{h} \mathrm{d}y $$
である。したがって、\(y\) 方向の重心位置は、
\begin{align}
\begin{split}
y_\mathrm{G} &= \frac{1}{M} \int_{0}^{h} y \, \mathrm{d}m \\[0.5em]
&= \frac{2}{\rho w h} \int_{0}^{h} y \, \rho \frac{w(h-y)}{h} \mathrm{d}y \\[0.5em]
&= \frac{2}{h^2} \int_{0}^{h} (hy-y^2) \mathrm{d}y \\[0.5em]
&= \frac{2}{h^2} \left[ \frac{1}{2}hy^2 – \frac{1}{3}y^3 \right]^h_0 \\[0.5em]
&= \frac{2}{h^2} \cdot \frac{1}{6}h^3 \\[0.5em]
&= \frac{1}{3}h
\end{split}
\end{align}
と求まる。ということは、三角形の重心は中線上にあり、かつ高さ方向の位置は、ある辺を底辺としたときの高さの1/3である。つまり、重心は中線を2:1に内分することが分かる。
さらに、三角形の各頂点の座標を \(x_\mathrm{i}, y_\mathrm{i}\) としたときの重心の座標を考えてみる。
点Pは辺BCの中点だから、その座標は
$$ (\mathrm{P}_x, \mathrm{P}_y) = (\frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2}) $$
である。重心は中線APを2:1内分するから、その座標は
\begin{align}
\begin{split}
(\mathrm{G}_x, \mathrm{G}_y) &= (\dfrac{1 \cdot x_1 + 2 \cdot \dfrac{x_2 + x_3}{2} }{2+1}, \dfrac{1 \cdot y_1 + 2 \cdot \dfrac{y_2 + y_3}{2} }{2+1}) \\[0.5em]
&=(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3})
\end{split}
\end{align}
となる。
奇妙なことに、三角形の場合、一様な密度を持つ薄板 (質量が板の面積に比例) の三角形を考えたときの重心と、同質量の3つの質点が頂点A, B, Cにそれぞれあるだけの剛体を考えた場合の重心の座標は一致する。
では、一様な密度を持つ薄板から構成された三角形と、質量が無視できるほど小さい丈夫な板から構成した三角形の各頂点に等しい質量の重りを接着したものがあったとして、両者の三角形の総質量が同じ場合、我々は区別できるだろうか。もちろん、外見は同じとする。それぞれの重心の位置は、前述のように全く同じである。
実は、区別することができる。それは、回してみることである。重心から遠い位置に質量が分配されているほど、回しにくい。このような回しにくさを、慣性モーメントという。
ところで、3次元の物体の重心 \(\boldsymbol{r_\mathrm{G}}\) は、以下で求められる。
\begin{align}
\begin{split}
\boldsymbol{r_\mathrm{G}} &= \frac{1}{M} \int \boldsymbol{r} \mathrm{d}m \\[0.5em]
&= \frac{1}{M} \int \rho \boldsymbol{r} \mathrm{d}V
\end{split}
\end{align}
複雑な形状に対して計算するのは難しいが、実験的には容易に求める方法がある。簡単のため、薄板で構成される形状を考える。
この物体上の任意の点を画鋲で刺すなどして、その点周りに回転できるようにして固定する。また、その点から重りを付けた糸を垂らし、重力に平行となる線を引く。次に、向きを変えて同じことをする。これらの直線の交点が、重心である。
なぜこうなるかは、重心の本質を理解していれば分かる。重心とは、重力の合力の着力点であるから、注目する物体への重力が、全てその重心に働くと考えても良い。仮に、重心が別のポイント \(\mathrm{G}^\prime\) にあり、赤直線上に無かったとする。力のつり合いを考えると下図のようになる。画鋲で固定した点には、重力と反対向きで大きさの等しい抗力が働いている。しかし、これらは同一直線上になく、モーメントが存在して回転しようとするから静止できない。したがって \(\mathrm{G}^\prime\) は重心ではない。重心ならば、必ず直線上にくる。
この方法は、薄板の面密度に分布があったり、穴が開いていたりしても成り立つ汎用性の高い方法であることに注意する。なお、3次元形状に対しても同様の方法で重心を決定できるが、物体内部を貫く直線を普通は見られないしマーキングすることもできない。