1. 概要
子供から大人まで、これが嫌いという人には会ったことがない、今回のテーマはカレーライスである。
家庭料理からキャンプ料理と、簡単に作ることができる定番メニューだが、凝りだすと奥は深い。
俺が初めてカレーライスを作ったのは、一人暮らしを始めた大学1年のことだった。市販のカレールーを使い、箱の裏に書いてある説明どおりに作ったのだが、失敗している。失敗の原因を細かく説明しないが、つまるところ、何ら定量化されていない従来の非料理工学に基づくレシピにより、俺は失敗したのである。料理など、人類が文明を築くはるか昔から行われた作業なのだが、なぜか、未だに感覚的表現が多く用いられる。料理の上手な人を増やさないために、わざとこんな表現を用いているのだとも考えられる。伝統技能や秘伝技術はそういう風に伝えるものがあることは理解するが、たかが料理ではないか。
料理ができない原因は、このような従来のレシピが蔓延っているからであると断言する。料理は、つまるところ、化学反応である。投入する材料の質量を測る、温度を測る、時間を測る、そして得られたデータを考察し改良する、たったこれだけで、従来とは一線を画すレシピが完成する。
玉ねぎ1個、人参1本、塩ひとつまみ、といった、従来のレシピを破壊し、料理工学に基づくカレーライスのレシピを、ここに公開する。なお、食材に含まれる水分のみを使う、いわゆる「無水カレー」のレシピである。
2. 作業内容
2.1 材料
| 材料/調味料 | 質量 [g] | 質量計算式 [g] | 質量例 [g] A=600 | 許容誤差 | 備考 |
|---|---|---|---|---|---|
| 玉ねぎ | $$ A $$ | 適用範囲: \( 580 \leq A \leq 600 \) | $$ A=600 $$ | $$ – $$ | 中サイズで約3個。 新玉ねぎも可。 |
| にんじん | $$ B $$ | $$ 0.2A $$ | $$ 120 $$ | $$ \pm 10 \% $$ | 中サイズで約1本。 |
| セロリ | $$ C $$ | $$ 0.16A $$ | $$ 96 $$ | $$ \pm 10 \% $$ | 約0.5本。 葉の部分も用いてよい。 |
| 鶏モモ肉 | $$ D $$ | $$ 0.48A $$ | $$ 288 $$ | $$ \pm 15 \% $$ | |
| じゃがいも | $$ E $$ | $$ 0.16A $$ | $$ 96 $$ | $$ \pm 10 \% $$ | 中サイズで約0.5個。 |
| (参考) 材料の合計 | \( M \) \( ( A \sim E\) の合計\( ) \) | $$ 2A $$ | $$ 1200 $$ | $$ – $$ | |
| 以下、調味料 | |||||
| S&B 赤缶カレー粉 | $$ a $$ | \( 0.009M \) \( (0.018A) \) | $$ 10.8 $$ | $$ \pm 0.1 \mathrm{g} $$ | 材料の合計質量の0.9% |
| 伯方の塩 DRY (鶏モモ肉用) | $$ b $$ | \( 0.01D \) \( (0.0048A) \) | $$ 2.9 $$ | $$ \pm 0.1 \mathrm{g} $$ | 鶏モモ肉の1% |
| 伯方の塩 DRY (最後の調整用) | $$ c $$ | \( \gamma – b \) \( (0.0052A) \) | $$ 3.1 $$ | $$ \pm 0.1 \mathrm{g} $$ | 伯方の塩DRY 合計から、鶏モモ肉用を除いた量 |
| (参考) 伯方の塩 DRY 合計 | $$ \gamma $$ | \( 0.005M \) \( (0.01A) \) | $$ 6.0 $$ | $$ – $$ | 材料の合計質量の0.5% |

(a):S&B 赤缶カレー粉 37g

(b):伯方の塩 DRY
図2.1-1:調味料
前述のように、本カレーライスは「無水カレー」のレシピである。今回用いる鍋「STAUB」は比較的容易に無水調理を行えるが、材料の水分量と鍋に占める材料の合計質量に注意しないと失敗しやすい。本レシピの水分の根幹となるのは「玉ねぎ」であり、この質量をAとして、その他材料/調味料の基準としている。材料の合計が2Aであるから、玉ねぎの質量割合は なんと50%である。
玉ねぎの質量Aは、多ければ多いほど水分が多くなり、失敗の可能性は小さくなるものの、今回用いる鍋「STAUB La Cocotte Round 20cm」では、A>600g とすると、体積的に他の材料が入らなくなる恐れがあり、A=600g は ほぼ限界値であると考えてよい。Aの最小値については、俺は 500g 以上から試しており、A=550g 以上で、水不足からくる失敗はほぼ無くなるが、マージンを考慮して580g としている。もっとも、水不足の場合は、加熱途中で水を足せば問題ないのだが、加えるタイミングや量の統一的な扱いが難しいので、本レシピでは、途中で注水を要しないように、十分量の玉ねぎを用いることにしている。
なお、「新玉ねぎ」を用いてもよく、通常の玉ねぎより水分量が多いため、失敗しにくい。新玉ねぎとは、乾燥させる前の玉ねぎである。したがって、通常の玉ねぎは、これを乾燥させたものである。
にんじん は香味野菜であり、カレーのスパイスと合うことと、火を通すと甘味が出るため、カレーの甘味付けの効果がある。この甘味は、無水調理することで一段と際立つ。玉ねぎの甘味も際立つが、本レシピでは、玉ねぎは最終的に溶けて形状が無くなるので、玉ねぎ本来の甘味に気づくのは難しいだろう。
セロリをカレーに入れるのは珍しいと思うが、香味野菜の一つなので、カレーのスパイスとよく合い、鶏肉の臭み消しにもなる。
鶏モモ肉は、あらかじめカットされている物を選ぶとよい。一口大で、唐揚げ用として売られているものが最適である。もちろん、大きな塊を買って自分でカットしてもよいが、まな板や包丁が汚れて面倒なのと、カンピロバクターによる食中毒を起こす可能性がある。また、食中毒で済めばまだよいが、稀に、手足の麻痺や顔面神経麻痺、呼吸困難などを起こす「ギラン・バレー症候群」を発症する場合がある。このように、生肉は意外と危険なので、慣れない人は生肉の加工を行うべきではない。
じゃがいもは、とろみ をつけるためだけのものである。すりおろして入れるので、じゃがいもの品種は問わない。
調味量としては、カレー粉と塩だけ使う。市販のカレールーを使う手もあるが、カレー粉の方が取り扱いが容易で味がシンプルなので、採用している。なお、いずれの調味料も、メーカによって適量が異なるために、品名を明記している。これ以外の調味料を用いた場合の味は 一切保証しない。
また、油を使わないので、何も考えないと焦げ付く恐れがあるが、次に示すように加熱工程を工夫することでそれを防いでいる。油も調味料の一つであり、カレーの味を決めるものでもあるが、料理工学標準の設計方針に基づき、油を使わないレシピとした。
本サイトで扱う料理についての設計方針を以下に示す。
1. 再現性のあるレシピが作成できる内容とする。
料理工学標準
2. 工程数は極力少なくする。
3. 一般的な食品店で入手できる素材のみを使う。
4. 調味料(特に油/塩)は極力使わない。(健康のため)
許容誤差について、基準となる玉ねぎは 適用範囲:580 \(\leq\) A \(\leq\) 600 として、その他の材料/調味料には上記表に示す通りの値を設定した。俺の試したところ、材料は基本的に ±10% で問題ないことを確認している。鶏モモ肉のみ ±15% と比較的大きいが、これは、店で販売されている鶏モモ肉の質量に合わせるためである。店での販売質量は、1パック当たり約250~350g 程度であり、かなりバラつきが大きい。レシピの質量を守るために鶏モモ肉を残してしまうことは、その後の取り扱いに困るので、買った1パックをそのまま使えるように考えた。大抵は、パックのラベルに質量が記載されているので、レシピの標準値 (0.48A) に近いものを購入すればよいだろう。
2.2 機器
| 機器 | 詳細 | 備考 |
|---|---|---|
| 鍋 | STAUB La Cocotte Round 20cm | 図2.2-1(a) |
| ボウル(大) | 藤井器物製作所 3way水切りボウル | 図2.2-1(b) |
| ボウル(小) | 下村企販 ボウル 小分け 容器 3個組 | 図2.2-1(c) |
| 質量計 | TANITA デジタルクッキングスケール KJ-212 | 図2.2-1(d) |
| ピーラー | VICTORINOX(ビクトリノックス) ユニバーサルピーラー レッド 縦型 皮むき器 | 図2.2-1(e) |
| おろし金 | パール金属 Easy Wash 食洗機対応 PCおろし器Sタイプ | 図2.2-1(f) |
図2.2-1:使用する機器
鍋/ボウル(大), (小)/質量計は、料理工学標準に定めるものと同じである。本レシピでは、ピーラーおよびおろし金を追加して使用する。
ボウル(大)は、材料の水洗いや計量に使う。図2.2-1(b)に示すものは汎用性が高く頑丈なので、おすすめする。
ボウル(小)は、調味料の計量に使う。図2.2-1(c)に示すものは1個当たりの質量は約51g と軽く、0.1g の計量が必要となる調味料に最適である。
ピーラーは、にんじん/じゃがいも の皮むきに使う。一般的には横型のものが多いが、図2.2-1(e)に示すような縦型もあり、個人的には縦型の方が使いやすく感じる。ナイフと同じような持ち方で扱うことができる。自分が使っているものは、図2.2-1(d)のものと同じく、VICTORINOXのものである。使い勝手は非常によい。
おろし金は、じゃがいも のすりおろしに使う。自分が使っているものと同じものは、web上で見つからなかったため、相当品を図2.2-1(f)に示す。商品を選ぶに当たり、特に気を付けるポイントは無い。
2.3 工程
- 玉ねぎの根と頭の部分を、1cm程度切り落とし、周方向に半分に切る。
- 白い中身が出るように手で皮をむく。
- この段階でボウル(大)を用いて質量を計測し、580g~600g となる玉ねぎの個数を概算しておく。
- 最初に半分に切ったものを、さらに周方向に半分に切り、1/4サイズにする。
- 中心軸に垂直に、約8mm幅で切る。
- 580g~600gとなるように、ボウル(大)で質量を計測し、1~5の工程を繰り返す。
- 全量を鍋へ入れる。このとき、適切な量であれば、鍋の縁から5cm程度まで埋まるはずである。
- 切断後の余った玉ねぎは、ラップで包み冷蔵庫へ保管する。(本レシピでは使用しない)

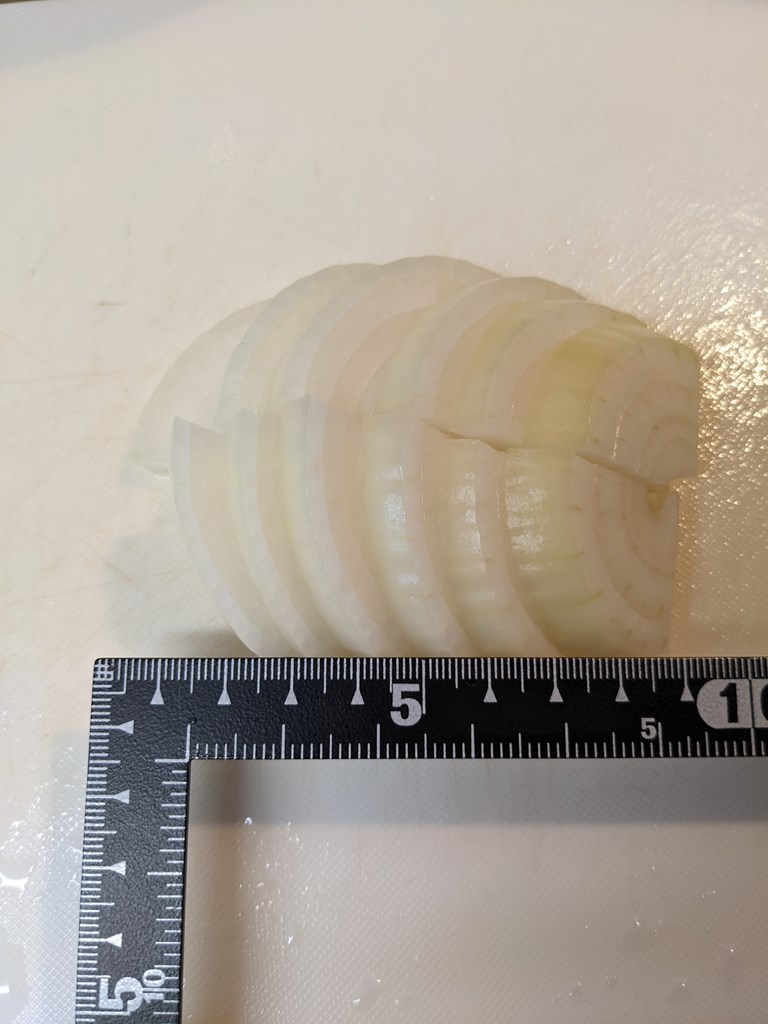

図2.3-1:玉ねぎの加工
- にんじんを水洗いし、ボウル(大)を用いて1本の質量を計測する。目標質量2Aとなる軸方向位置を予測し、切断する。
- ピーラーで皮をむく。
- 周方向に1/2に切る。
- 中心軸に垂直に、約5mm幅で切る。
- 2Aとなるように質量を計測し、不足分は1.の残りから切り出す。
- 全量を鍋に入れる。
- 切断後の余ったにんじんは、ラップで包み冷蔵庫へ保管する。(本レシピでは使用しない)



図2.3-2:にんじんの加工
- セロリを水洗いし、枝の別れ目の位置で切断する。ボウル(大)を用いて茎の質量を計測する。
- 茎の質量が目標質量0.16A以上であれば、0.16Aとなる軸方向位置で切断する。0.16A未満であれば、葉を加えて調整する。
- 茎は、軸に平行に1/2に切断する。
- 茎/葉とも、斜め45degにして、約8mm幅で切る。
- 全量を鍋に入れる。
- 切断後の余ったセロリは、ナイロン袋に入れて冷蔵庫で保管する。(本レシピでは使用しない)


図2.3-3:セロリの加工
- じゃがいも1個を水洗いし、質量を計測する。目標質量0.16Aとなるように切断する。
- 皮をむき、ラップに包んでおく。(すりおろし工程は後で実施する。すりおろし後は変色が酷いため。)
- 鶏モモ肉をボウル (大) に入れて、質量を計測する。
- 鶏モモ肉の質量の1% (0.0048A相当) の塩をボウル (小) を用いて軽量し、ボウル (大) へ入れて鶏モモ肉に満遍なくなじませる。
- 材料の合計質量2Aの0.9% (0.018A相当) のカレー粉を、ボウル (小) を用いて軽量し、ボウル (大) へ入れて鶏モモ肉に満遍なくなじませる。
- 全量を鍋に入れる。



図2.3-4:鶏モモ肉の加工
- 蓋を開けて、全体的にかき混ぜる。(弱火のまま)
- 最後の調整用の塩として、ボウル(小)を用いて、材料の合計質量2Aの0.5%から鶏モモに要した塩を差し引いた分 (0.0052A相当) を計量し、鍋へ入れてかき混ぜ、蓋を閉める。(弱火のまま)
- step4で予備加工したじゃがいもをすりおろし、蓋を開けて鍋へ入れる。
- 蓋を開けたまま、中火へ切り替え、焦げ付き防止のため 5分間かき混ぜ続ける。

(a):手順1のかき混ぜる前の状態

(b):手順1のかき混ぜた後の状態

(c):手順3のすりおろしたじゃがいも

(d):手順3のすりおろしたじゃがいもを加えた状態

(e):手順4が完了した状態
図2.3-6:味付け工程
図2.3-6(a) に示すように、蓋を開けた直後は、水分が足りないように見えるが、かき混ぜることで鍋底にあった水分が出てくる。なお、手順2で入れる塩の効果によって、さらに水分が引き出され、最終的には図2.3-6(e) のように、丁度よい水分量となる。
- 火を止めて蓋を閉め、30分間放置する。
- ジップロック等の保管容器に移し、冷蔵庫で10時間以上保管する。保管限度は48時間まで問題ないことを確認しているが、極力早めに次stepにて消費すること。

図2.3-7:保存容器に移した状態
- 冷蔵庫に保管していたカレーを、消費する分だけ取り出して鍋に入れる。
- 蓋を開けて中火で加熱する。焦げ付き防止のため、かき混ぜ続ける。全体的に沸騰してきたら完成である。(目安:10分)

図2.3-8:カレーライスの完成
3. 料理工学的観点から
工程、いわゆるレシピは2章に示すとおりである。本節では、工程を決めるに至った理由を、料理工学的観点から述べる。この部分は、世にあるレシピが最も蔑ろにしている箇所でもある。一つ一つの手順には、必ず理由が存在すべきで、理由が無い手順は削除されるべきである。また、順番も重要であり、どの順番でもよくて適当に並べているだけなのか、その順番でなければ完成品に致命的な欠陥がおよぶのか、も理由をつけて識別すべきである。
工学上、ある製品の製作に必要な全ての情報を示したものが「図面」である。これさえあれば、コピー品を作ることができる。しかし、何か変更をしたい場合、例えば、(a) 軽量化のために部品の寸法を縮小したい (b) コスト低減のために別の材料で代替したい (c) 工程を減らすために手順を省略したい、という要望が出てきた場合、それを実施してよいかどうか、すなわち、それらの変更を行うことで、製品が従来と同等の機能や安全性を持つかどうか、図面からは判断できないことが多い。
このような判断のためには、「設計情報」が必要になる。なぜその材料を使ったか、なぜそのような手順が必要か、という情報は、コピー品の製作には不要な情報なので、通常は図面に書かない。そのような情報は「設計情報」として秘匿される場合が多い。例えば、図面に書かれたその寸法や手順を決めるために、その会社で過去に数百万円、数千万円かけて要素試験を実施し、その結果から判断して決めた値かもしれない。そういう観点から、設計情報というのは、膨大なデータであったり、人が考えた過程でもあるから、技術的価値の高いものであると言ってよいだろう。
2章の作業内容が「図面」に相当し、本省に示す内容は「設計情報」に相当する。本記事を読んでレシピを再現する人がいるかどうか分からないが、一度作ってみると、アレンジしたくなるのが人の性である。材料にトマトやリンゴを入れたらどうなるか、切り方を変えたらどうなるか、じゃがいもの代わりに小麦粉を使うとどうなるか、油を使うとどうなるか、実際試してみるのが簡単だと思うが、毎回試して決めるのは時間が掛かるし、失敗/成功したにしても、その理由を考えることが重要である。そこを考えることこそ、料理工学の根幹であり、従来の料理を超越する行動である。以下に示す内容が、何らかの参考になれば幸いである。
3.1 材料の切断
なぜ切るのか、考えたことはあるだろうか?
- そもそも鍋に入らないから切る
- 口に入らないから切る
- 嚙みにくいから繊維を切る
- 火が通りにくいから切る
考えられる理由はこんなところだと思う。1~3 はそのとおりで、これ以上問い詰めようがないが、4は少し漠然としている。「火が通りにくいから」を、もう少し分解してみる。
我々は、小さく切ると火が通りやすいことを経験的に知っている。「小さく切る」という行為は、つまるところ、「単位体積当たり、または単位質量あたりの表面積を大きくする」行為である。
例えば、代表長さ \( L \) の立方体を考える。単位体積あたりの表面積 (比表面積という) をαとすると、
$$ \alpha_\mathrm{cube} = \frac{L^2 \times 6}{L^3}=\frac{6}{L} \tag{3.1-1} $$
である。すならち、代表長さ \( L \) が小さいほど \( \alpha \) は大きくなることが分かる。形状が半径 \(L\) の球の場合、
$$ \alpha_\mathrm{sphere} = \frac{4 \pi L^2}{\frac{4}{3} \pi L^3}=\frac{3}{L} \tag{3.1-2} $$
となる。このように、形状が相似であれば、\(\alpha\) は \(1/L\) に比例する。これは、面積は \(L^2\) に比例し、体積は \(L^3\) に比例することからも明らかである。
$$ \alpha \propto \frac{1}{L} \tag{3.1-3} $$
さて、上記は体積に注目したが、体積と質量は比例関係にあるので、同様の議論は単位質量当たりにも言えることである。
比表面積が大きいことと、火が通りやすいことにどのような関係があるか、だが、料理において、材料の表面積はほぼ伝熱面積に等しい。例えば、茹でられている材料を簡易的に考えて、材料の外表面が100℃に保たれていると見做す (*1) 。すると、材料の中心部をある温度に到達させるのに要する時間は、明らかに比表面積の大きい方が有利である。
このように、「切る」という行為を細分化してみた。実際の料理では、複数の材料を使うから、料理の完成状態において、火の通り具合を同程度にしたいのである。しかし、材料毎に比表面積が同じでも火の通りやすさが異なるから、切り方を変えなければならない。
このような前提のもとで、2.3節で示した、材料毎の切り方の理由を以下に示す。
3.1.1 玉ねぎ
玉ねぎは、無水カレーとなる本レシピにおける、主水分である。そのため、水分の出やすい切り方のとして、繊維方向に垂直に切る。あとは、火が通りやすい大きさに切ればよく、それが中心軸に平行に1/4サイズにした後、約8mm幅で切る理由である。もっとも、1/4以上に分割したり、8mm以下の幅に細かく切ってもよいが、俺が試した範囲では、これ以上細かく切っても完成状態への影響は軽微であった。したがって、最小手順としてこのように定めた。
1. 玉ねぎの根と頭の部分を、1cm程度切り落とし、周方向に半分に切る。
2.3節より抜粋
2. 白い中身が出るように手で皮をむく。
3. この段階でボウル(大)を用いて質量を計測し、580g~600g となる玉ねぎの個数を概算しておく。
4. 最初に半分に切ったものを、さらに周方向に半分に切り、1/4サイズにする。
5. 中心軸に垂直に、約8mm幅で切る。
3.1.2 にんじん
にんじんの皮は向かなくてもよい、という意見もあるが、土の中の細菌や、長期保存の場合はその細菌に伴うカビが付着していることが多く、また食感も硬いため、皮は必ずむく。
2. ピーラーで皮をむく。
2.3節より抜粋
にんじんは、火が通りにくい材料である。そのため、玉ねぎよりは細かく、約5mm幅で切る。周方向に1/2するのは、一口サイズにするためである。先端部ほど細いので、比表面積をそろえるために、先端近傍は周方向に分割しなくてもよいし、先端を分割する場合は幅を5mmより大きくしても良い。
3. 周方向に1/2に切る。
2.3節より抜粋
4. 中心軸に垂直に、約5mm幅で切る。
3.1.3 セロリ
セロリは繊維が硬い。そのため、繊維を断ち切るように切る必要がある。
手順1にて枝の分かれ目で切断する理由は、単純に長すぎるからである。
手順2にて葉よりも茎を優先して使う理由は、茎の方が味も歯ごたえも多いためである。
手順3にて軸に平行に1/2に切断する理由は、一口サイズにするために行う。
手順4にて斜め45gegにする理由は、垂直だとサイズが小さすぎるためである。幅は8mm以下でもよいが、あまり小さくすると溶けて食感が無くなってしまう。また、これ以上幅を大きくすると火が通りにくく繊維も残るため、食べにくくなる。
1. セロリを水洗いし、枝の別れ目の位置で切断する。ボウル(大)を用いて茎の質量を計測する。
2.3節より抜粋
2. 茎の質量が目標質量0.16A以上であれば、0.16Aとなる軸方向位置で切断する。0.16A未満であれば、葉を加えて調整する。
3. 茎は、軸に平行に1/2に切断する。
4. 茎/葉とも、斜め45degにして、約8mm幅で切る。
3.2 鶏モモ肉の加工
まず、なぜカレーの具として鶏肉を使うかというと、低脂質で高タンパクのためである。その観点では胸肉でもよいが、パサつくのでモモ肉を用いている。なお、鶏肉には独特の臭みがあり、これを消すための工程が手順2, 3である。
なお、手順2, 3において、鶏モモ肉へ塩とカレー粉を同時にかけてはいけない。必ず塩を満遍なくなじませてから、カレー粉の手順へ移行すること。
2.鶏モモ肉の質量の1%(0.0048A相当)の塩をボウル(小)を用いて軽量し、ボウル(大)へ入れて鶏モモ肉に満遍なくなじませる。
2.3節より抜粋
3.材料の合計質量2Aの0.9%(0.018A相当)のカレー粉を、ボウル(小)を用いて軽量し、ボウル(大)へ入れて鶏モモ肉に満遍なくなじませる。
なお、臭い消しとして、あらかじめ塩で洗うという方法もあるが、以下のとおり、生肉の加工は極力避けるべきである。湯通しする手もあるが、こちらは手間が大きい。
まな板や包丁が汚れて面倒なのと、カンピロバクターによる食中毒を起こす可能性がある。また、食中毒で済めばまだよいが、稀に、手足の麻痺や顔面神経麻痺、呼吸困難などを起こす「ギラン・バレー症候群」を発症する場合がある。このように、生肉は意外と危険なので、慣れない人は生肉の加工を行うべきではない。
2.1節より抜粋
カンピロバクターについては、以下が参考になる。本レシピでは、材料の加工工程のうち、鶏モモ肉の加工を一番最後に配置している。これは、何らかの要因で、まな板や他の材料に鶏モモ肉が付着する可能性を低減するためである。

図3.2-1:消費者向けリーフレット 家庭調理の心得
(出典:厚生労働省)
3.3 加熱工程
1. 鍋に蓋をして、弱火で15分加熱する。
2.3節より抜粋
2. 中火に切り替えて、蓋の隙間から蒸気が出るまで加熱する。(目安:6分)
8分を超えても蒸気が出ない場合は何かがおかしい。蒸気を見逃している可能性があるため、8分を限度として次の手順へ移る。
3. 弱火に切り替えて20分加熱する。
手順1の弱火15分加熱は、本レシピでは鍋底に油を敷かないので、焦げ付き防止のためのものである。しかし、何故油を敷くと焦げ付きを防止できるのだろうか?これは意外に難問である。
一般に、油を敷くと、鍋~食材への熱伝達が向上して火の通りが良くなると言われる。物理的に接触している表面は、細かな凹凸があり、表面が均一に接触しているわけではない。その空隙には熱伝導率の小さな空気が入っているため、例え金属同士の接触であっても、熱伝達にとって抵抗となり、熱が伝わりにくくなる。これを「接触熱抵抗」という。油を敷くと、その隙間に油が充填され、空気より熱伝導率が大きいため、接触面間の接触熱抵抗が小さくなる、という仕組みである。
それでは、接触熱抵抗が小さいことと、焦げ付きにくことは、関係があるか評価してみる。
一般的には接触熱抵抗を \( R \, \mathrm{[K/W]}\) とし、単位通過熱量当たりの温度差として表現される。すなわち、接触熱抵抗が大きいと、同じ熱量を通す場合、より多くの温度差を生じてしまうことを意味する。なお、議論しやすくするために、単位面積当たりに換算した接触熱伝達係数 \( h_\mathrm{contact} \, \mathrm{[W/(m^2 \cdot K)]} \) を定義する。これは、接触面積を \( A \, \mathrm{[m^2]} \) として、
$$ h_\mathrm{contact} = \frac{1}{RA} \tag{3.3-1} $$
と表せる。
余談だが、熱抵抗という考え方は、自分としてはしっくりこないものがある。熱抵抗は、電気回路と同じように熱回路を表現するために用いるものだが、電気と熱の考え方は、本質的に異なる箇所がある。それは、電気では「電気の通しにくさ」を指標として単位が作られているのに対し、熱は「熱の通しやすさ」を指標として単位が作られている点である。例えば、電気抵抗は「電気の通しにくさ」を意味しているが、熱伝導率は「熱の通しやすさ」を意味する。すなわち、熱の単位は、分子に熱量がきて、分母に面積や温度がくることが多い。そんな中、熱抵抗はこれと逆で、\( R \, \mathrm{[K/W]}\) という単位であり、他の熱に関する単位とは逆数のようになっている。したがって、これだけ異質に見えるのである。そこで、熱屋としては、\( R \) の逆数を熱結合値 \( G \, \mathrm{[W/K]} \) と定義してこちらを用いて考える方が自然である。しかし、世の中的には、熱を専門としない人にとっては、「熱抵抗」の方が意味が伝わりやすいというジレンマがある。
図3.3-1に示すように、食材を入れた鍋を火にかけて加熱する現象を簡単に考えると、ガスの炎から鍋底へ、鍋底から食材へ、食材から外囲環境へ、という一連の熱の流れがあると考えられる 。ただし、図3.3-1では、便宜上 高さ方向を横向きに取っている。
図3.3-1:鍋で食材を加熱する熱モデル
ここで、
\begin{alignat}{3}
&T_\mathrm{fire} & \quad & \colon \; 炎の温度 & \qquad \qquad \qquad & \mathrm{[K]\,or\,[^\circ \mathrm{C}]} \\
&T_\mathrm{pot} & \quad & \colon \; 鍋の温度 & \qquad \qquad \qquad & \mathrm{[K]\,or\,[^\circ \mathrm{C}]} \\
&T_\mathrm{food} & \quad & \colon \; 食材の温度 & \qquad \qquad \qquad & \mathrm{[K]\,or\,[^\circ \mathrm{C}]} \\
&T_\mathrm{\infty} & \quad & \colon \; 外囲環境の温度 & \qquad \qquad \qquad & \mathrm{[K]\,or\,[^\circ \mathrm{C}]} \\
&h_\mathrm{fire} & \quad & \colon \; 炎と鍋の熱伝達係数 & \qquad \qquad \qquad & \mathrm{[W/(m^2 \cdot K)]} \\
&h_\mathrm{contact} & \quad & \colon \; 鍋と食材の接触熱伝達係数 & \qquad \qquad \qquad & \mathrm{[W/(m^2 \cdot K)]} \\
&h_\mathrm{\infty} & \quad & \colon \; 食材と外囲環境の熱伝達係数 & \qquad \qquad \qquad & \mathrm{[W/(m^2 \cdot K)]} \\
&A & \quad & \colon \; 伝熱面積 & \qquad \qquad \qquad & \mathrm{[m^2]}
\end{alignat}
である。なお、簡単のため、定常状態とし、鍋や食材などの内部の温度分布は考慮しない (一つの温度で代表する) こととする(*1)。また、図中の〇/△印は各部位の代表温度を、緑線は熱結合値をそれぞれ示す。なお、△印は温度境界であり、条件によって変わらない固定値である。すなわち、〇印で示した \(T_\mathrm{pot} \), \( T_\mathrm{food} \) が未知数であり、これを求めていくことになる。そして、これらの温度は既知の値の関数となるはずである。その式が求まれば、\(h_\mathrm{contact} \) を変更したときの各部温度への影響を定量的に評価することができる。
定常状態では熱流束 \(q \, \mathrm{[W/m^2]}\) が一定であるから、
\begin{align}
\begin{split}
& 炎~鍋 \hspace{25mm}& q &= h_\mathrm{fire} ( T_\mathrm{fire} {}- T_\mathrm{pot} ) \\[0.5em]
& 鍋~食材 \hspace{25mm}& q &= h_\mathrm{contact} ( T_\mathrm{pot} {}- T_\mathrm{food} ) \\[0.5em]
& 食材~外囲環境 \hspace{25mm}& q &= h_\mathrm{\infty} ( T_\mathrm{food} {}- T_\mathrm{\infty} )
\end{split}
\tag{3.3-2}
\end{align}
となる。式\(\text{(3.3-2)}\) では \(q\) の表現方法は3つあるが、\(T_\mathrm{pot}\) や \(T_\mathrm{food}\) といった未知数を用いずに \(q\) を表現したい。つまり、既知である \(T_\mathrm{fire}\) と \(T_\mathrm{\infty}\) の温度を用いて表現できれば、取り扱いが容易となる。整理するのは厄介に見えるが、
$$(T_\mathrm{fire}- T_\mathrm{pot}) + (T_\mathrm{pot}- T_\mathrm{food}) + (T_\mathrm{food}- T_\mathrm{\infty})= T_\mathrm{fire}- T_\mathrm{\infty} \tag{3.3-3} $$
となるから、式 \(\text{(3.3-2)}\) の両辺の逆数をとって足し合わせると、
$$ q = \cfrac{T_\mathrm{fire} – T_\mathrm{\infty}}{\cfrac{1}{h_\mathrm{fire}} + \cfrac{1}{h_\mathrm{contact}} + \cfrac{1}{h_\mathrm{\infty}}} = K ( T_\mathrm{fire} {}- T_\mathrm{\infty} ) \tag{3.3-4}$$
を得る。ここで、
$$K= \cfrac{1}{h_\mathrm{fire}} + \cfrac{1}{h_\mathrm{contact}} + \cfrac{1}{h_\mathrm{\infty}} \tag{3.3-5}$$
として、\(K \, \mathrm{[W/(m^2 \cdot K)]}\) を熱通過率という。
以上のように \(q\) が既知となったので、未知数であった \(T_\mathrm{pot}\), \(T_\mathrm{food}\) は次のように表せる。
\begin{align}
\begin{split}
&T_\mathrm{pot} &= T_\mathrm{fire} -\frac{q}{h_\mathrm{fire}} \\[0.5em]
&T_\mathrm{food} &= T_\mathrm{pot} -\frac{q}{h_\mathrm{contact}} = T_\mathrm{fire} – q \left( \frac{1}{h_\mathrm{fire}} + \frac{1}{h_\mathrm{contact}} \right)
\end{split}
\tag{3.3-6}
\end{align}
これで定量評価の準備は整った。適当な値を代入して、\(h_\mathrm{contact}\) の各部温度への影響を評価してみる。
しかし、あまりに適当な値を入れるのもセンスがないので、ある程度現実的な値を入れるようにする。
ガスコンロの炎の温度は、木原らによると 1700~1900℃ 程度である。ただし、これは火炎の最高温度であり、鍋底が全て炎に当たっているわけではないから、鍋底に当たる炎の平均温度としてはこれより確実に低いだろう。炎の最高温度1800 ℃ 、外気温度 20℃ として、平均をとると910℃、ざっくり900℃と見做すことにする。
また、森田ら (2012) によると、炎~鍋の熱伝達係数は 100~160 [W/(m2.K)] 程度、鍋~水の熱伝達係数は 3000~7000 [W/(m2.K)] 程度である。後者について、水は流動性があるから、通常の食材だとこの値より小さくなると考えられる。3000~7000 の平均値 2500 のざっくり半分程度と見込み、鍋~食材の熱伝達係数は1200 [W/(m2.K)] とする。
食材~外囲環境の熱伝達係数 \(h_\mathrm{\infty}\) は、対流熱伝達としては数十程度の値だが、食材の水分蒸発などがあるので、やや大きめにみて 100 [W/(m2.K)] とした。
以上の情報から、感度評価のデフォルト値を次のように設定する。
\begin{align}
\begin{split}
&T_\mathrm{fire} &= 900 & \mathrm{[^\circ \mathrm{C}]} \\[0.5em]
&T_\mathrm{\infty} &= 20 & \mathrm{[^\circ \mathrm{C}]} \\[0.5em]
&h_\mathrm{fire} &= 130 & \mathrm{[W/(m^2 \cdot K)]} \\[0.5em]
&h_\mathrm{contact} &= 1200 & \mathrm{[W/(m^2 \cdot K)]} \\[0.5em]
&h_\mathrm{\infty} &= 100 & \mathrm{[W/(m^2 \cdot K)]}
\end{split}
\tag{3.3-7}
\end{align}
\(h_\mathrm{contact}\) をいくつか変更して、各部温度への影響を評価した結果を図3.3-2に示す。
図3.3-2:鍋~食材間の接触熱伝達係数の各部温度への影響
食材の温度に注目すると、\(h_\mathrm{contact}\) が小さいほど、食材温度は低くなる。式\(\text{(3.3-2)}\) に示すように、\(h_\mathrm{contact}\) は熱抵抗 \(R\) と逆数の関係にあるから、「熱抵抗が大きいほど食材温度は低い」と言える。これだけ見ると、食材が高温化しないのだから焦げ付きにくいということになってしまう。
一方、鍋の温度は食材温度とは異なり、「熱抵抗が大きいほど鍋温度は高い」と言える。結局、鍋と食材の温度差ΔTは \(h_\mathrm{contact}\) の逆数に比例しており、熱バランスを保つように各部温度が決まっている、ということである。
ところで、熱流束 \(q\) をプロットしたものを図3.3-3 に示すが、\(h_\mathrm{contact}\) が大きいほど、\(q\) も大きい。鍋に油を敷くことは \(h_\mathrm{contact}\) を大きくすることに対応しており、結果として \(q\) が大きくなると言える。すなわち、油を敷いた方が食材に熱がとおりやすくなるということを、定量的に示している。
図3.3-3:鍋~食材間の接触熱伝達係数の熱流束への影響
さて、鍋と食材の温度差について、今一度考えてみる。これらの接触面を模式的に表したものを図3.3-4に示す。
赤線は温度分布を示しており、物体表面の凸凹が存在する狭い領域で、急激に温度差が生じる。前述の評価では、この部分を接触熱抵抗とみなし、この狭い領域が無限に薄く、温度が不連続となるような分布を考えていたことになる。しかし実際は、鍋の最低温度は食材温度に近い部分もあるかもしれないし、逆もまた然りである。つまり、食材の最高温度は、鍋の温度と等しくなる部分もあるかもしれない。「かもしれない」というのは、これは物体表面の凸凹に依存するからであって、如何なる物理的接触面に対して言えることではないためである。ただし、鍋や食材の表面凸凹はとても大きいはずだから、このような可能性を考えることは非現実的ではないだろう。
図3.3-4:接触面近傍の温度分布
以上より、焦げ付きの原因は接触熱抵抗だという仮説は、接触面近傍における食材温度の高温化のため、と言える。しかしながら、平均温度としては接触熱抵抗の大きい方が食材温度が低い、ということも事実であり、この仮説が正しいかは疑う余地がある。例えば、次のような思考実験を考える。
全く同じフライパンを2つ用意し、片方には油を敷く。両方とも同じ温度になるまで熱して、同時に生卵を落とし入れる。この場合、油を敷かないフライパンは直ちに焦げ付いてしまうことが容易に想像できる。これは過渡状態であり、生卵を落とし入れてから数秒で変化が見られるだろうから、前述のように、熱抵抗によってフライパン温度が高温化する時間的余裕はない。また、フライパンの熱容量は生卵より圧倒的に大きいこともあり、この数秒間では、フライパンの温度は変化せず両者とも同じと見るべきだろう。ということは、熱抵抗の小さい方がΔTが小さいので、生卵の温度は油を敷いた方が高温となる。なのに焦げ付かない。これはしかし、どう考えたものか。
一旦、焦げ付き=高温 という観点から離れてみよう。そもそも、焦げ付くということは、「焦げる」ことと「付着する」こと双方を指している。焦げることは高温化のためだろうが、付着は別の観点が必要そうである。そもそも、鉄のフライパンの他に、テフロン加工したものがあり、素材として焦げ付きにくいものが存在している。つまり、素材によって付着力が異なると考えるのが自然である。
そんなことを考えながら、ネットの海を彷徨っていると、次のような説明があった。
油をひかず鉄製のフライパンや鉄板焼きの鉄板を使用すると、食材がこびりつきます。
この理由は、鉄板の表面に吸着水という目には見えない水の薄い膜があるからです。鉄板に食材を載せると食材の水溶性成分がこの表面水の中に溶け出します。この成分が熱によって固まると、食材と鉄板が直に接着しておこげの原因となります。
このようにならないためには、※吸着水の上に油の層を作る(油をひく)、あるいは吸着水を持たないものでコーティング(テフロン加工)すればよい。
※中国料理の「鍋ならし」「油ならし」は、先に中華鍋に火を入れることで吸着水を蒸発させ、その後、油を入れ層を作るテクニックである。
料理化学の森
なるほど。確かにこれが正解なのだろう。しかし、「吸着水」の存在を示す根拠は、ネット上では見つけることができなかった。おそらく分子間力で鉄原子と結合していると思われるが、そのような論文は誰か書いていないのだろうか。
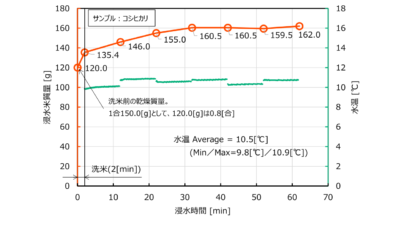
ところで、本レシピでは、油を敷かない代わりに、弱火15分の加熱を行うことで焦げ付きを回避している。これは実験的に見出した条件であるが、後付けの理由としては、食材からの水分を鍋底に貯めて、鍋底近傍で「煮込み」に近い状態を作り出しているためである。実際に温度を計測しており、試験セットアップを図3.3-5に、温度計測結果を図3.3-6にそれぞれ示す。なお、熱電対は蓋の取っ手を外した孔より差し込んでおり、測温接点部は鍋の温度を拾わないように、鍋底から数mm浮かせている。また、試験時の玉ねぎの質量は A=590g、材料全体の質量は M=1183g である。

図3.3-5:試験セットアップ
図3.3-6:温度計測結果 (加熱工程)
0~15分まで弱火加熱を行っている。途中温度が下がるが、これは熱電対の測温接点を鍋底から数mm浮かせており、そこは玉ねぎの集積部であるから、玉ねぎから出てきた水分に浸かったり浸からなかったりするためだと考えられる。15分後には安定して100℃を示しているから、測温接点位置まで水分に満たされたと言えるだろう。この結果から、弱火加熱時間を15分と設定している。
15分以降蒸気が出るまで中火としており、今回の試験では約6分間の中火加熱にて蒸気が確認された。その後は弱火加熱を行っている。
3.4 寝かせる工程
そもそも、寝かせる工程を行わなくても、もちろん食べることができる。しかし、カレー粉の味が材料に十分しみ込んでおらず、また鶏モモ肉の臭みも十分に消えていないので、本工程を経ることを推奨する。
1. 火を止めて蓋を閉め、30分間放置する。
2.3節より抜粋
2. ジップロック等の保管容器に移し、冷蔵庫で10時間以上保管する。保管限度は48時間まで問題ないことを確認しているが、極力早めに次stepにて消費すること。
また、手順1にて長時間常温放置することは、食中毒の観点から行ってはいけない。
加熱後調理で気を付けるべき食中毒として「ウェルシュ菌」があり、カレーの材料になる肉や魚介類、野菜に付着している。
ウェルシュ菌 (食品安全委員会のページ) は熱に強く、100℃で数時間加熱しても完全に殺菌することはできない。また、広範囲の温度域 (12~50℃、至適温度:43~45℃) で増殖することが知られている。したがって、保存時はこの温度帯を避けて、10℃以下または55℃以上とする必要がある。以下のウェザーニュースの記事も参考のこと。
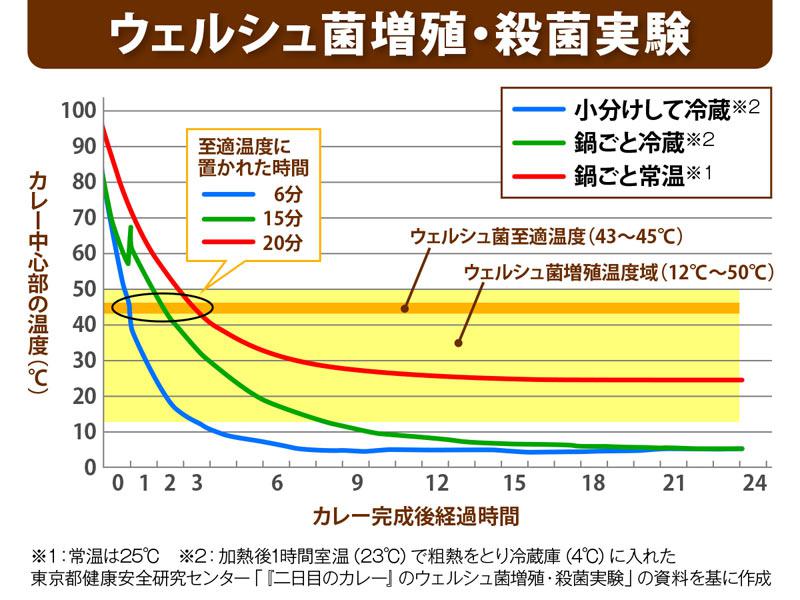
図3.4-1:加熱しても要注意 カレーの食中毒予防法
(出典:ウェザーニュース)
手順1の30分の根拠は、実際に温度を計測した結果に基づいている。
手順1にて、熱電対をカレーに差し込み、蓋をして常温環境下に放置した。試験セットアップは前節にて示した図3.3-5と同じで、温度トレンドを図3.4-2にそれぞれ示す。なお、熱電対は蓋の取っ手を外した孔より差し込んでおり、測温接点部は鍋の温度を拾わないように、鍋底から数mm浮かせている。
常温放置を開始してから30分で約80℃となり、開始時の100℃から20℃低温化した。前述のように、ウェルシュ菌の増殖温度範囲上限は55℃であるが、今回は鍋を五徳の上という比較的断熱環境で放置したことや、外囲環境温度の低い冬場では冷却速度が大きくなることを考慮し、十分な温度マージンを確保し、常温放置時間の最大値を30分とした。
図3.4-2:温度計測結果 (カレー常温放置)
保存容器に移す状態で80℃程度あるが、このまま冷蔵庫へ入れる。なお、冷却速度を上げて危険温度帯にいる時間を少なくするために、なるべく小分けの容器に入れる。適当な容器があればもっと小分けにする方が望ましい。俺の場合、毎回図2.3-7の容器で2分割保存し、一般的な冷蔵庫で冷却しているが、食あたりを起こしたことはないので、問題ないと思われる。
3.5 再加熱工程
1. 冷蔵庫に保管していたカレーを、消費する分だけ取り出して鍋に入れる。
2.3節より抜粋
2. 蓋を開けて中火で加熱する。焦げ付き防止のため、かき混ぜ続ける。全体的に沸騰してきたら完成である。(目安:10分)
再加熱に電子レンジを使う方法もあるが、均等に熱が入らず、表面だけ焦げたりするので、鍋を使う加熱としている。なお、米を炊くのを忘れないように注意。炊飯の詳細はこの記事を参照のこと。
4. おわりに
今回のレシピは、STAUBを使った料理を紹介している「ずぼら料理教室」さんのYoutube動画を参考としている。
図4-1:無水カレー ストウブ簡単バージョン@ずぼら料理教室