1. 概要
自炊を始めたのは大学生のころだった。
最初の頃はネットで見たレシピを参考に簡単な料理をしてみるのだが、うまくいかないのである。
例えば、うどんを作ろうとして、クックパッドの適当なレシピを見る。(図1-1)
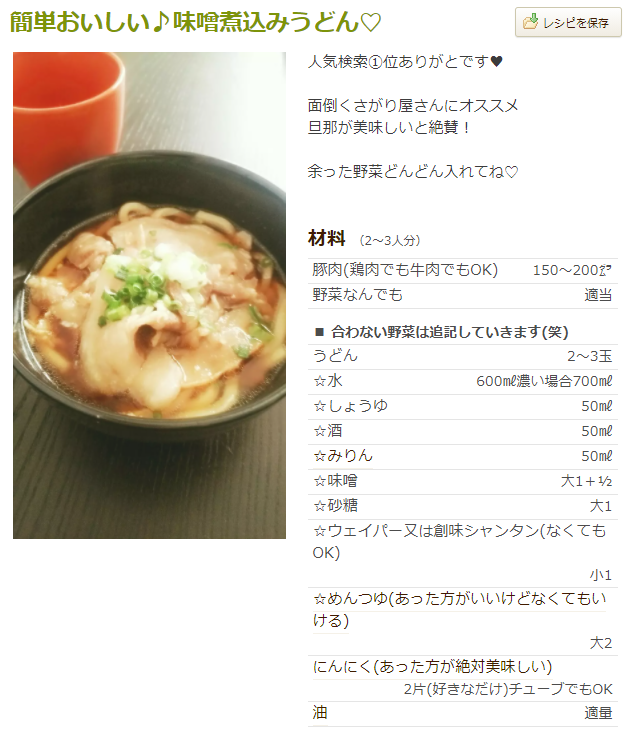
図1-1:レシピ例
料理経験のない人間からすると、次のような疑問が浮かぶ。
- 肉、野菜、なんでもOK、とは、本当になんでもよいのか、野菜の分量はどれくらいなのか?
- 酒とは、日本酒なのか?
- みりんって何だ? (その後みりんを知るが、「本みりん」と「みりん風調味料」があることに気づくだろう)
- 味噌も味がいろいろある
- 大さじって何だ カレー用の大きいスプーンで適当に測ればいいのか
- めんつゆ なくてもいいならレシピに書かなくてよいのでは?
- 油 サラダ油/オリーブ油/ごま油/etc… 適量とは?
これはまだ材料ページであり、作り方には進んでないのにこれだけの不明点がある。
うどん一つでここまでヤバいのである。俺の知っているうどんは、もっと簡単なもののはずだった。
別にこのレシピに恨みがあるわけでは全くなく、世の中に出回っているレシピはほとんどこんな感じであり、俺は料理をあきらめた。結局いつも作るのは、ゆで卵や目玉焼き、野菜炒め、鍋といったシンプルなものに限られる。
料理のできる人から見れば、こういうレシピはよく分かるのだと思う。
それは料理の経験であり、センスであり、料理を楽しむ、ということらしい。
しかしどうだろう。料理を一つの工学品と見るならば、それを作り上げる工程は「誰が見ても」明確に記載できるはずだし、その料理は「誰が作っても」完全に再現できるはずなのだ。
すなわち、従来レシピは工学的観点からの「手抜き」がある。それを埋めるのが料理の経験やセンスなのだろう。
考えてみれば、料理は本質的に多くのばらつきを内包している。例えば「にんじん1本」は、大きいものから小さいものまで様々である。レシピ作者は大きめのにんじんを使って「1本」と書いたのならば、それを再現するときも同じ大きさのにんじんを使わなければならない。
こういうときは質量で記載すべきなのだ。にんじん100gと書けば、一意に定まってしまうのである。ただ、○○gと言われてもピンとこないので、にんじん100g(大きめのにんじんならば1/2本相当)と補足すればよい。
こういう曖昧な料理を完全に過去のものにし、誰が作っても同じ結果となるような、そんな料理を目指していく。
計測に基づき、料理を工学的観点で再構築する。ここに「料理工学」なる学問が誕生する。
2. 用意するもの(計測機器)
料理工学を進める上で、質量計は欠かせない。その次に温度計があるとよい。
2.1 質量計
あらゆる材料の質量を計測するために、質量計は必要不可欠である。料理工学では、にんじん1本とか、砂糖大さじ1という表現を許可せず、すべて質量で表現する。
どの程度の質量を計測できればよいか、というと、上限は1kg程度、下限は0.1g程度でよいだろう。
1kgは通常家庭で料理する際に十分な量であり、0.1gは調味料を測るときに必要である。
料理をすると分かるが、塩1gは驚異的な量であるので、0.1g単位の計量は不可欠である。
しかし、1kgに対して0.1gを計測する、というのは実は結構難しいのである。
1gに対して0.1gを計測するならば、その比は1/10なので、その感度をもつセンサーを使えばよい。
しかし1kg=1000gに対して0.1gは1/10000であるから、1万分の1の変化を感知できるセンサーが必要となる。
キッチン用質量計として、様々なものが販売されているが、最小軽量単位は1gのものが多い。それ以上の精度はマジ物の質量計となり、価格も桁が1つか2つ跳ね上がってしまう。
そんな中、TANITAから良さそうな質量計が販売されている。

図2.1-1:TANITA デジタルクッキングスケール KJ-212
最大2kg計量、最小単位は0.1g(ただし200g以下)であり、上記要求は満たす。価格は2千円程度である。俺はこれを買った。
使い勝手は特に問題ない。
2.2 温度計(熱電対)
具材の温度は何℃なのか、鍋底の温度は何℃なのか、これらを知ることは、その後の料理が成功したか失敗したかという情報と合わせて、貴重なデータとなる。考えてみれば料理とは、温度の管理なのである。
しかし、常に温度計測するのは困難であり、また計測できたところでそれを再現するのは難しい。例えば野菜炒めの作り方で、「フライパンの底部温度を350℃に保ち、具材を10分間炒める」という書き方にしたとしても、それを再現できるユーザは、同様に温度計測しながら確認しなければならず、非現実的である。火加減については、従来どおり、弱火/強火といった情報で伝えるしかないのだろうが、それにしても弱火ではフライパンの底が250℃で、強火だと400℃になった、という情報は後々の料理をするうえでありがたいデータとなる。
また、弱火/強火の定義だが、これは次のように定義することで、統一的に扱えるだろう。
- 弱火:火が消えない最小ガス流量
- 強火:なべ底から火がはみ出ない最大ガス流量
- 中火:弱火と強火の指示値の半分のガス流量
強火はコンロの最大ガス流量でなく、使用するなべ底の直径で制限を設けることで、コンロ固有のばらつきを低減している。もっとも、なべ底からはみだす火力は取っ手を損傷してしまうのでそんな火力は使用しないのだろうが。
ガス種による違い(都市ガス/プロパン)も考えられるが、一般家庭用コンロはどちらのガスでも同程度の火力になるように調整されているので、ガス種の違いは考えなくてよい。
さて、上記のように温度計測はあくまで参考データ扱いなので必須ではないが、「料理工学」をガチる上では、揃えておきたい。
要求条件は以下である。
- 測定温度:0~800℃程度。
- 時系列データを記録できること。
- センサ部は細く、応答性が良いこと。
800℃は、炎の温度を測ってみたい、という欲望からである。通常のなべ底温度はここまで高温にならない。
時系列データについては、料理は昇温/降温速度も重要だからである。「弱火でじっくり/強火で一気に」の違いである。
センサ部については、いくら精度のよいセンサでも、センサ部からの熱逃げが大きいと、測定対象部の温度を拾えなくなるためである。また、センサ部の熱容量が大きいと急峻な温度変化を検知できなくなってしまう。理想的にはセンサ部は極小で、極細線でセンサ部と計測機器をつなぐのが良い。
話がずれるが、料理に限らず温度計測は想像以上に難しい。一つには上記のように測定対象部とセンサの温度を一致させることの難しさがある。
小学校の理科の授業で棒温度計を使って水の沸点を計測したと思うが、棒温度計は、内部の液体(赤色に着色された白灯油が多い)を全て測定対象温度と同じにしたとき、正しい温度を示すように作られている(一部例外あり)。すなわち、液だめ部のみ測定対象(例えば沸騰した水)に浸没させて計測する方法は不可で、正しくは全長を浸没させなければならない(例外として、浸没ラインを定めるものがある)。
これは棒温度計の測定原理が内部液体の温度に対する体積膨張率を読み取っているからであり、内部液体の全領域が測定対象温度と等しくなければならないからである。
一方、上記計測方法を忠実に実行したとしても、水温が急激に変化する場合(例えば50℃/min)、この棒温度計の指示値は正しく追従してくれるのだろうか。棒温度計自体の熱容量によって、その指示値は実際の水温より一歩遅れて応答することは想像に難くないだろう。
長さや質量といった基本単位の中でも、「温度」は計測が難しい方に入ると思う。
そもそも「温度」は説明するのがとても難しい物理量である。温度計で測ったものが温度と言うかもしれないが、上記の棒温度計では、温度によって変化した体積膨張率を読み取っているに過ぎない。すなわち、温度は体積膨張させる力を持った何かである、としか言えないのである。
熱力学的には、温度とはエントロピーと表裏一体の物理量であり、この「エントロピー」もまた説明が難しい物理量であるが、それ以上のことは熱力学では何も答えてくれない。その本質は、統計熱力学や量子力学でようやく明らかになってくるのだが、未だに研究されている分野であり、特にエントロピーという単語は様々な場面で耳にすると思う。自分はこのエントロピーに関連する研究が、時間の概念や重力、ひいては宇宙の成り立ちに至るまで、いつの日か解明してくれると思っている。
現代においては、多少の科学技術の進歩ではあまり驚かなくなってしまった。電気のない時代に電気を作った、蒸気機関を作った、核エネルギーを見つけた、というようなものと同じレベルの衝撃は、現代では、時間の概念の解明(タイムトラベル可能か)、重力の解明などの、宇宙に関する大いなる謎の解明しか無いような気がしている。
温度計測や熱力学にまつわる内容は、別記事で書きたいと思うが、ようは温度計測は大変なのである。たかが料理といえど、料理工学としてガチるためには妥協できない部分である。
市販されているキッチン用温度計は高々250~300℃が測定上限である。2.1項で素晴らしい質量計として挙げたTANITAの温度計を見てみよう。
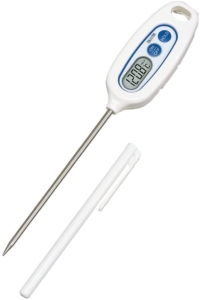
図2.2-1:TANITA 料理用スティック温度計 TT-508N
最高250℃まで計測できる。一般的な料理の温度としては十分であるが、測定部が太くて感度が悪そうなのと、なべ底の温度を計測したりはできなさそうである。天ぷら油の温度確認くらいしか使えないだろう。
別の温度計として、工学的な温度計測としてよく用いられる熱電対を使うことにしよう。
熱電対(ねつでんつい, thermocouple)とは、金属に温度勾配を与えると電位差が生じる現象を利用した温度計である。2種類の金属を同じ温度勾配に置き、一方の端部を電気的に接合した場合、開放部である他端には温度差に対応した電位差が生じる。この電位差を計測することで温度に換算する。
熱電対は上記原理をスマートに応用した計測器であり、原理詳細は別記事「熱電対の原理」に示す。
2種類の金属の組み合わせとしてよく用いられるのはクロメル/アルメルを用いるものである(type K)。
また、熱電対素線を金属細管で保護した「シース熱電対」という形態がよく用いられる。見た目は1本の針金に見えるのだが、内部は酸化マグネシウム(MgO)などの絶縁物とともに細い熱電対素線が2本入っている。大人になって仕事で使うときに初めてこのシース熱電対の存在を知ったのだが、「1本しか素線が無いのになぜ温度が計測できるのだろう」と不思議に思ったものである。
amazonで探してみる。シース径は細ければ応答速度が向上して良いのだが、断線しやすくなる。だいたいの価格として、type Kのシース熱電対は1本5千~1万円くらいである。結構高いのである。よって、多少の断線しにくさを考慮しつつ、応答速度もよいものとして、シース径はφ1mmとする。

図2.2-2:アズワン K熱電対(シース型) KTO-10300C φ1x300mm
俺はこれを買った。仕事では腐るほど使ってきたが、個人的に買ったのは人生初である。
しかし、これだけでは計測できない。先ほど述べたように、電圧を計測して温度に換算しなければならない。そして、それを時系列データとして記録しなければならない。
そのような装置を一般に「データロガー」という。
そしてクソ高い。まともな物は10万~20万、あるいはそれ以上する。
既製品を買わずにマイコン等で自作する、という手もあるのだが、今はそこまで気力がないので、適当なデータロガーの検索を続ける。そして出会った。

図2.2-3:アズワン K熱電対データロガー RX-450K
- 計測ch:1ch
- 測定精度(25℃):±0.8℃(熱電対の誤差は含まず)
- 測定間隔:5~59秒・1~240分
なるほど、極限までシンプルにしたデータロガーだ。
お値段は2万円である。なんでだろう、10万とか20万する汎用データロガーを見ていたら、ずいぶん安く感じてしまうではないか。買ってしまった。
結局、温度計測のためには熱電対(約6千円)とデータロガー(約2万円)、消費税10%も考慮すると3万円弱かかってしまった。
俺は、ただ、料理がしたいだけなんだ。
ところで、この熱電対とデータロガーの組み合わせの精度は、というと、
- 熱電対単体の精度:クラスが不明だが、クラス2とすると、-40℃以上 333℃未満において±2.5℃
- データロガーの精度:25℃において±0.8℃
- 熱電対+データロガーの精度:約±3.3℃
となる。なんと、まじめに誤差を積み上げると約3℃もずれる可能性がある。
しかし、適当な温度定点に対する誤差を計測することによってある程度補正できる。例えば、0℃における指示値が1℃、100℃における指示値が101℃であった場合、0~100℃の範囲における誤差は+1℃程度と考えられるので、計測値から1℃差し引いた値はほぼ真値となる。このような作業を校正という。
身近に達成できる温度定点は0℃/100℃の2つなので、これを使って今回の温度計の校正をしてみよう。
まずは0℃の温度定点だ。最終的な試験セットアップを図2.2-4に、製作過程を図2.2-5に示す。
サーモスの真空断熱タンブラーに、細分化した氷と僅かな水を入れて、熱電対計測部(先端部)において水の融点0℃を目指す。
まず、熱電対シースからの伝導熱リークによる影響を極力排除するため、可能な限りシースを長く浸漬させる。つまり、コップの底に触れないギリギリの位置に熱電対先端を固定する(底に触れると底の温度を拾うため)。
次に氷を充填していくが、可能な限り細かくする。これは、氷の比表面積を大きくして溶けやすい状態を作ることで、極力0℃の安定化を図っている。氷が意外と固く、最初はハンマーで叩き割ろうとしたのだがうまくいかず、包丁で叩き割る方法がやりやすかった。大体1cm各程度になれば十分だろう。コップの縁ギリギリまで充填する。
水を入れるのだが、入れすぎは禁物である。水を入れすぎて氷が浮くような状態となれば、熱電対先端付近は水しか存在しないことになる。現代に生きる我々は、水の密度は約4℃が最大であることを知っているのだから、このようにしてはいけない。すなわち、水は、氷が浮き上がらず、かつ熱電対シース部もある程度浸るような量にしなければならない。今回の試験系では、水は30g加えた。
最後に、コップにラップをかぶせる。これは、上面からの自然対流熱伝達を抑止している。つまり、断熱している。

図2.2-4:熱電対校正(0℃) 試験セットアップ





図2.2-5:熱電対校正(0℃) 試験セットアップ製作過程
このような状態で、温度計測を開始し、1時間程度放置する。その計測結果が図2.2-6である。
最後の10minを平均すると0.03℃であった。すなわち、かなり正確な指示値を出していることが分かる。なんだ、なかなか優秀な実力を持っているではないか。
ところで、ギザギザの振動が出ているが、現実に温度がこのように振動することは考えにくい。これはおそらく、機器側のノイズか、あるいはデータロガーのAD変換器の性能であると思われる。いずれにしても振幅は0.1℃未満なので、料理をする上ではゴミカスであるから気にしないこととする。
ちなみに水の融点は厳密には0℃ではない。もともとは水の融点を0℃として組み立てられた温度が「℃」であるが、その後の科学技術の発展により、より厳密な温度目盛りが考案されてきた。水の融点は圧力等の影響を受けるため、温度の定義点として用いるには都合が悪く、少し前のSI単位系の定義では、水の3重点の温度を0.01℃と定義していた。このように定義することで、融点の値がわずかに0℃からずれているのである。そして、2019年に改訂された新しい温度の定義は以下である。
ケルビン (記号は \(\rm{K}\)) は、熱力学温度のSI単位であり、ボルツマン定数 \(k\) を単位 \(\rm{J \, K^{-1}(kg \, m^2 \, s^{-2} \, K^{-1}}\)に等しい)で表したときに、その数値を \(1.380 \, 649 \times 10^{-23}\) と定めることによって定義される。
国際単位系 (SI) 第 9 版 (2019) 日本語版
これは、水の3重点を用いた定義における精度でも我慢できない人たちが出てきたために(狂気の世界で闘い続ける者たちの世界である)、新たに定義されたものである。もはや何を意味するか分からないと思うが、これも別記事で書きたいと思う。
図2.2-6:熱電対校正結果(0℃)
次は100℃の温度定点である。最終的な試験セットアップを図2.2-7に、製作過程を図2.2-8に示す。
使用した鍋は「STAUB La Cocotte de GOHAN 12cm」であり図2.2-9に示す。この鍋は鋳物であり、1kg以上と重く、熱容量も十分である(熱容量が大きいと、温度変化を吸収してくれるので、このような温度定点向けには都合が良い)。
余談だが、この鍋は炊飯に最適である。炊飯器を使うと毎回蓋とか洗うのがクソ面倒だが、これは本当にただの鍋なので洗うのが楽であり、また火を使うので料理をしているライブ感も味わえる。1万3千円くらいするが、買ってよかったもののひとつだ。
蓋には「熱電対を通してくれ」と言わんばかりの取っ手があるので、ドライバーで外す。熱電対先端が底部よりわずかに上に来るようにしてクリップで止める。あとは水を充填し、火にかけて沸騰を待つ。図2.2-8では、強火における沸騰状態を示すが、かなりの勢いで沸騰しており、このまま数十分放置するのはガスがもったいないので弱火とした。なお、弱火としても十分な沸騰を確認している。(写真ではマイナスドライバーで蓋を支えているが、demon core の実験を思い出してしまった。)

図2.2-7:熱電対校正(100℃) 試験セットアップ



図2.2-8:熱電対校正(100℃) 試験セットアップ製作過程

図2.2-9:STAUB La Cocotte de GOHAN 12cm
沸騰後、20minほど放置した結果を図2.2-10に示す。
最後の10minを平均すると100.49℃であった。これもまた、かなり正確な値を示していることが分かる。
結局、0℃における校正では+0.03℃の差異、100℃においては+0.49℃の差異であるから、0~100℃の範囲では約+0.5℃の誤差があると見てよいだろう。なかなか良い結果となった。
なお、100℃以上についての誤差は不明である。その気になれば錫の融点(231.9℃)や鉛の融点(327.5℃)で校正できるのだが、危ないのでやめておこう。100℃以上については、スペック誤差、すなわち±3.3℃と見ておけばよい。
なお、水の沸点も厳密に100℃ではないが、これは水の融点のことで書いたのと同じ話である。
(というか、気圧や不純物の影響で0.1℃程度は余裕で変化するので、今回の計測における真値が99.9743℃であったかは分からないが、おおよそ妥当だということにしておこう。)
図2.2-10:熱電対校正結果(100℃)
3. 計測例 (米浸水時間の妥当性)
準備が終わったので、計測例を書いてみる。米の浸水時間である。
洗米後に適当な時間浸水させないと上手く炊飯できないことは知られているが、一体何分浸水させればよいのだろうか。
「夏は20~30分、冬は60~90分くらい」等、かなり適当な表現しかみつからない。
北海道の冬と沖縄の冬は気温が全く違うのだが、それでも彼らはそうのように表現するのだろうか。
このような曖昧な表現を、料理工学で破壊してみよう。
まず、米の計量単位は通常「合」であるが、これは体積を表しており都合が悪い。一般に、粉粒体の充填率はばらつきがあり、例えばトントンと衝撃を与える「タッピング」を行うと、充填率が大きくなることが知られている。すなわち、同じ1合でも質量が異なってしまう。
いくつかweb検索した結果に基づき、1合=150gと定義する。
俺は0.8合が一回の食事に丁度良いので、0.8合=120gを用いて試験を行った。
なお、米はコシヒカリを用いた。試験セットアップを図2.3-1に示す。

図2.3-1:米浸水時間評価用 試験セットアップ
洗米を2minとし、その後10min間隔で水を切り、米の質量を計測した結果を図2.3-2に示す。
なお、質量計測のための時間は2minとし、その時間は浸水時間に含めていない。
水温は平均10.5℃であり、約30minで米の質量変化はほとんど無くなった。
つまり、水温10.5℃においては浸水時間は30min以上で問題ない。
水温が変わる場合はどうか、と問われると、
- 水温が10.5℃より高い場合:一般的に反応速度は高温ほど速いので、浸水時間は30minで十分である。急ぎたい場合、おおざっぱな検討では、アレニウスの式(10℃ 2倍則)を適用し、水温20.5℃ならば浸水時間は0.5倍の15min程度で十分と考えられる。
- 水温が10.5℃より低い場合:30min以上を要するが、おおざっぱな検討では、アレニウスの式(10℃ 2倍則)を適用し、水温0.5℃ならば浸水時間は2倍の60minを要すると考えられる。
- 上記をまとめると、水温が0℃以下はありえないのだから、すべての条件(あらゆる水温)を満たす浸水時間は60min以上と考えられる。ただし、実測は10.5℃で行ったため、0℃近傍や20℃などの条件での精度を高めるには、その温度における実測が望ましい。
これが料理工学である。
図2.3-2:浸水時間と米質量の関係




